Bondy Murty Graph Theory Exercise 1.2.2

Exercise 1.2.2

These are the solutions to the exercises of the book Graph Theory with Applications by J. A. Bondy and U. S. R. Murty.

(a) If $G\simeq H$ , then there exist bijections $\theta : V(G)\rightarrow V(H)$ and $\phi : E(G)\rightarrow E(H)$ such that $\psi_G(e)=uv\iff\psi_H (\phi(e))=\theta(u)\theta(v)$ .

Since $\theta$ is a bijection, $\lvert V(G)\rvert=\lvert V(H)\rvert$ . Hence $\nu(G)=\nu(H)$ .

Similarly, since $\phi$ is a bijection, $\lvert E(G) \rvert=\lvert E(H)\rvert$ . Hence $\epsilon(G)=\epsilon(H)$ . $\square$

(b) Consider the following example:

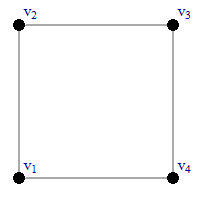
$G$

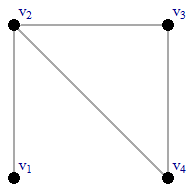
$H$

Here $\nu(G)=\nu(H)$ and $\epsilon(G)=\epsilon(H)$ but $G$ and $H$ are not isomorphic.

The solutions of all the exercises of “Graph Theory with Applications” by J. A. Bondy and U. S. R. Murty, are available for download as a pdf file! Click the button below.