Exercise 1.2.12
These are the solutions to the exercises of the book Graph Theory with Applications by J. A. Bondy and U. S. R. Murty.
(a) By Exercise 1.2.5, an automorphism of a simple graph G exists if there is a bijection \sigma : V(G)\rightarrow V(G) such that: uv\in E(G)\iff \sigma (u) \sigma (v)\in E(G).
Since \sigma is a bijection from set to itself, then by definition \sigma is a permutation. Thus an automorphism can be regarded as a permutation of the vertex set that preserves adjacencies.
In group theory, it is known that the set of permutations of a set is a group under the operation of composition. Thus since the set of automorphisms is a non-empty subset of the set of all permutations of the vertex set, in order to show that the set of automorphisms is a group, we just need to check for the closure and inverse properties.
Let \Gamma(G) denote the set of automorphisms of G.
Closure: Let \sigma_1,\sigma_2\in \Gamma (G).
Therefore:
\begin{aligned}uv\in E(G)\iff \sigma_1(u)\sigma_1(v)\in E(G)\iff \sigma_2(\sigma_1(u))\sigma_2(\sigma_1(v))\in E(G)\end{aligned}and similarly,
\begin{aligned}uv\in E(G)\iff \sigma_2(u)\sigma_2(v)\in E(G)\iff \sigma_1(\sigma_2(u))\sigma_1(\sigma_2(v))\in E(G)\end{aligned}Thus \sigma_2\sigma_1\in \Gamma (G) and \sigma_1\sigma_2\in \Gamma (G).
Inverse: Let \sigma\in \Gamma (G). Consider the permutation \sigma^{-1}:V(G)\rightarrow V(G) where \sigma^{-1}(\sigma(u))\rightarrow u.
Let u,v \in V(G). Therefore u=\sigma (x) and v=\sigma (y) for some x,y\in V(G) and xy\in E(G)\iff \sigma(x)\sigma(y)\in E(G), since \sigma \in \Gamma (G).
Hence \sigma^{-1}(u)\sigma^{-1}(v)\in E(G)\iff uv\in E(G). Therefore \sigma^{-1}\in \Gamma(G).
(b) The automorphisms of K_n are all the possible permutations of the vertex set V(G). We can write \Gamma (K_n)=S_n where S_n is the set of all the permutations of \lbrace 1,2,\cdots,n\rbrace.
Regarding the complete bipartite graph K_{m,n}, consider two cases.
Case 1: m\neq n
Case 2: m=n
In Case 1, the automorphisms are all the permutations that map the vertices of one part (of the partitions) into vertices of that same part. Hence the automorphisms of K_{m,n} are all the combinations of S_m and S_n, which can be written as S_m\times S_n.
In Case 2, the automorphisms include all the automorphisms mentioned for Case 1. However it also includes those permutations which map all the vertices of one part into the other, and vice versa.
(c)
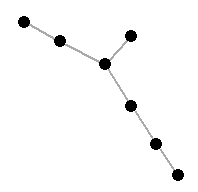
(d) Let \sigma\in\Gamma (G). Hence \sigma is a bijection on the vertex set of G such that:
\begin{aligned}uv\in E(G)&\iff \sigma(u)\sigma(v)\in E(G)\\uv\notin E(G)&\iff \sigma(u)\sigma(v)\notin E(G)\\uv\in E(G^c)&\iff \sigma(u)\sigma(v)\in E(G^c)\end{aligned}Hence \sigma\in \Gamma (G) and \Gamma(G)\subseteq\Gamma(G^c). Similarly it can be shown that \Gamma(G^c)\subseteq\Gamma(G) . \square
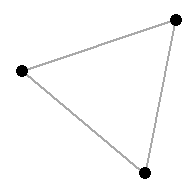
(e) There are 4 non-isomorphic simple graphs on 3 vertices. The following two graphs have 6 automorphisms:

The following two graphs have 2 automorphisms:
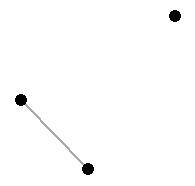
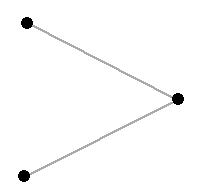
Hence result follows. \square
(f)
The solutions of all the exercises of “Graph Theory with Applications” by J. A. Bondy and U. S. R. Murty, are available for download as a pdf file! Click the button below.