Univerity of Malta

FEMA

Business Statistics 1

Past Paper Solutions





  • How to use the Catalogue


    Go the filter bar on the top and choose the solutions you want to access by Year and Topic. For example in the following we are choosing the questions for all years related to the topic of Disrete Distributions.



    The list of questions that satisfy the filters set above, are shown on the left of the screen. For example.



    Now choose a question from the list on the left.



    The solution of the chosen question will then be displayed in the middle of you screen. For example:


  • Year 2021 Question 1

    a)
    \begin{aligned} \int_{-\infty}^{\infty} f(x) dx&=1\\ \int_0^4 k(x^2-3x+4) dx&=1\\ k\int_0^4 x^2-3x+4\ dx&=1\\ k\bigg[\frac{x^3}{3}-\frac{3x^2}{2}+4x\bigg]_0^4 dx&=1\\ k\bigg[\bigg(\frac{4^3}{3}-\frac{3(4^2)}{2}+4(4)\bigg) -\bigg(\frac{0^3}{3}-\frac{3(0^2)}{2}+4(0)\bigg)\bigg] dx&=1\\ k\bigg(\frac{40}{3}\bigg)&=1\\ k&=\frac{3}{40} \end{aligned}

    b)
    \begin{aligned} P[a\leq X \leq b]&=\int_a^b f(x) dx\\ \therefore P[0.2\leq X \leq 3.2]&=\int_{0.2}^{3.2} \frac{3}{40}(x^2-3x+4)dx\text{ (since }k=\frac{3}{40})\\ &=\frac{3}{40}\int_{0.2}^{3.2} x^2-3x+4\ dx\\ &=\frac{3}{40}\bigg[\frac{x^3}{3}-\frac{3(x^2)}{2}+4x\bigg]_{0.2}^{3.2} \\ &=\frac{3}{40}\bigg[\bigg(\frac{3.2^3}{3}-\frac{3(3.2^2)}{2}+4(3.2)\bigg) -\bigg(\frac{0.2^3}{3}-\frac{3(0.2^2)}{2}+4(0.2)\bigg)\bigg]\\ &=0.5715\\ &=57.15\% \end{aligned}

    c)
    \begin{aligned} E[X]&=\int_{-\infty}^{\infty} xf(x) dx\\ \therefore E[X]&=\int_{0}^{4} x(\frac{3}{40})(x^2-3x+4) dx\\ &=\frac{3}{40}\int_{0}^{4} x(x^2-3x+4) dx\\ &=\frac{3}{40}\int_{0}^{4} x^3-3x^2+4x\ dx\\ &=\frac{3}{40}\bigg[\frac{x^4}{4}-x^3+2x^2\bigg]_{0}^{4}\\ &=\frac{3}{40}\bigg[\bigg(\frac{4^4}{4}-4^3+2(4^2)\bigg)-\bigg(\frac{0^4}{4}-0^3+2(0^2)\bigg)\bigg]\\ &=2.4 \end{aligned}

    \begin{aligned} E[X^2]&=\int_{-\infty}^{\infty} x^2f(x) dx\\ \therefore E[X^2]&=\int_{0}^{4} x^2(\frac{3}{40})(x^2-3x+4) dx\\ &=\frac{3}{40}\int_{0}^{4} x^2(x^2-3x+4) dx\\ &=\frac{3}{40}\int_{0}^{4} x^4-3x^3+4x^2\ dx\\ &=\frac{3}{40}\bigg[\frac{x^5}{5}-\frac{3x^4}{4}+\frac{4x^3}{3}\bigg]_{0}^{4}\\ &=\frac{3}{40}\bigg[\bigg(\frac{4^5}{5}-\frac{3(4^4)}{4}+\frac{4(4^3)}{3}\bigg)-\bigg(\frac{0^5}{5}-\frac{3(0^4)}{4}+\frac{4(0^3)}{3}\bigg)\bigg]\\ &=7.36 \end{aligned}

    \begin{aligned} \therefore Var(X)&=E[X^2]-E[X]^2\\ &=7.36-2.4^2\\ &=1.6 \end{aligned}

    \begin{aligned} \therefore sd(X)&=\sqrt{Var(X)}\\ &=\sqrt{1.6}\\ &=1.265 \end{aligned}

    d) Since the range of X is 0\leq x \leq 4, then f(x)=0 for x\leq 0 and f(x)=1 for x\geq 4.

    For 0\leq x \leq 4 we have:
    \begin{aligned} F(x)&= \int_{-\infty}^x f(t)dt\\ \therefore F(x) &= \int_{0}^x \frac{3}{40}(t^2-3t+4)dt\\ &=\frac{3}{40}\int_{0}^x t^2-3t+4\ dt\\ &=\frac{3}{40}\bigg[\frac{t^3}{3}-\frac{3(t^2)}{2}+4t\bigg]_{0}^{x} \\ &=\frac{3}{40}\bigg[\bigg(\frac{x^3}{3}-\frac{3x^2}{2}+4x\bigg) -0\bigg]\\ &=\frac{x^3}{40}-\frac{9x^2}{80}+\frac{3x}{10} \end{aligned}

    Hence:

    F(x)=\begin{cases} 0 & x\lt 0 \\ \frac{x^3}{40}-\frac{9x^2}{80}+\frac{3x}{10} & 0\leq x\leq 4 \\ 1 & x\gt 4 \end{cases}

    e) The median is the number m such that F(m)=0.5.

    Hence we need to show that F(3.63)=0.5.

    \begin{aligned} &F(3.63)\\ =&\frac{3.63^3}{40}-\frac{9(3.63^2)}{80}+\frac{3(3.63)}{10}\\ =&0.8024^* \end{aligned}

    * Note that this value should be 0.5. This indicates that there is a mistake in the paper, because the median is not 3.83.

    f)
    \begin{aligned} Skewness &= \frac{3(Mean-Median)}{Standard\ Deviation}\\ &=\frac{3(2.4-3.63^*)}{1.265}\\ &=-2.917 \end{aligned}


    * Note that here we are using the (incorrect) median value provided in the paper.

  • Year 2021 Question 2

    a) (i) No, there is no need to introduce class boundaries in order to plot a bar graph. This is because a bar graph is ideal for categorical variables and discrete variables. A bar graph is made up of a number of non-touching bars, and thus class boundaries are not required.

    (ii) Yes, class boundaries need to be found in order to plot a histogram. A histogram is ideal for continuous variables. A histogram is made up of a number of touching bars, in which the bar touch on the class boundaries.

    b) In order to plot the histogram, we must define the classes (and thus their boundaries), their width and their estimated frequency. In order to find the estimated frequency of each class, we use the formula:

    \begin{aligned} Estimated\ frequency=\frac{Standard\ Width\times Frequency}{Width} \end{aligned}

    We will use a standard width of 2 (which is the minimum width of the classes).

    Temperature Frequency Class Width Estimated Frequency
    -20 to -10 3 -20.5\lt x \leq -9.5 11 0.55
    -9 to 0 10 -9.5\lt x \lt 0.5 10 2
    1 to 2 8 0.5\leq x \lt 2.5 2 8
    3 to 4 12 2.5\leq x \lt 4.5 2 12
    5 to 7 10 4.5\leq x \lt 7.5 3 6.67
    8 to 11 2 7.5\leq x \lt 11.5 4 1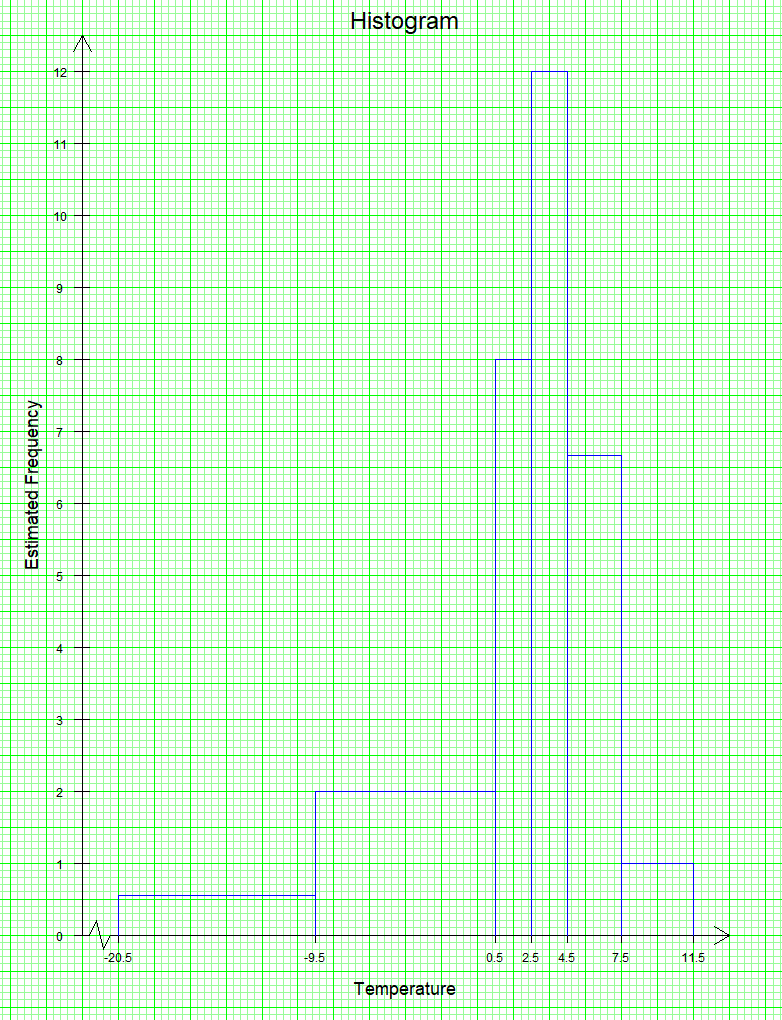
    HIstogram
    c)
    Class Class Mark
    -20.5\lt x \leq -9.5 -15
    -9.5\lt x \lt 0.5 -4.5
    0.5\leq x \lt 2.5 1.5
    2.5\leq x \lt 4.5 3.5
    4.5\leq x \lt 7.5 6
    7.5\leq x \lt 11.5 9.5


    d) The histogram and the frequency distribution show a distribution which is skewed to the left (that is, negatively skewed).

    e)
    Temperature Cumulative Frequency Cumulative Percentage
    x\leq -20.5 0 \frac{0}{45}=0\%
    x \leq -9.5 3 \frac{3}{45}=6.67\%
    x \lt 0.5 13 \frac{13}{45}=28.89\%
    x \lt 2.5 21 \frac{21}{45}=46.67\%
    x \lt 4.5 33 \frac{33}{45}=73.33\%
    x \lt 7.5 43 \frac{43}{45}=95.56\%
    x \lt 11.5 45 \frac{45}{45}=100\%

  • Year 2021 Question 3

    a) A suitable probability distribution is the Poisson Distribution. The corresponding probability distribution for X is:

    P[X=x] = \frac{\lambda^x e^{-\lambda}}{x!}\text{ for }x=0,1,2,3,\cdots

    In our example, the time unit is hours. Thus \lambda=150, that represents 150 arrivals per hour. Thus in our case, the probabililty distribution is:

    P[X=x] = \frac{150^x e^{-150}}{x!}\text{ for }x=0,1,2,3,\cdots

    We assume that arrivals are independent, from a very large population of cars (of infinite size). Each car has an equal but very small probability of arrival.

    b) Let "time unit"= "2 minutes" in this case. Thus:

    \lambda=\frac{150}{60}\times 2 = 5

    This is because by simple proportion, if on average 150 cars arrive in a 1 hour interval, then on average 5 cars arrive in a 2-minute interval.

    \begin{aligned} P[X\lt 3] &= P[X= 0]+P[X= 1]+P[X=2]\\ &=\frac{5^0e^{-5}}{0!}+\frac{5^1e^{-5}}{1!}+\frac{5^2e^{-5}}{2!}\\ &=0.1247\\ &=12.47\% \end{aligned}

    c) Let "time unit"= "4 minutes" in this case. Thus:

    \lambda=\frac{150}{60}\times 4 = 10

    This is because by simple proportion, if on average 150 cars arrive in a 1-hour interval, then on average 10 cars arrive in a 4-minute interval.

    \begin{aligned} P[X\gt 3] &= 1-P[X= 0]-P[X= 1]-P[X=2]-P[X=3]\\ &=1-\frac{10^0e^{-10}}{0!}-\frac{10^1e^{-10}}{1!}-\frac{10^2e^{-10}}{2!}-\frac{10^3e^{-10}}{3!}\\ &=0.9897\\ &=98.97\% \end{aligned}

    c) A suitable distribution is the Binomial Distribution. Its probability distribution is given by:

    P[Y=y] = \binom{n}{y}p^y(1-p)^{n-y}\text{ for }y=0,1,2,3,\cdots,n

    This results from the repetition of n independent trials and their is an equal probability p of success in each trial. In our case we have 250 cars, representing the 250 trials, thus n=250. Each car has a probability of \frac{15}{250}=\frac{3}{50}=0.06 of getting involved in an accident. Thus p=0.06, where a success is defined by a car getting involved in an accident in our example. Thus the probabililty distribution is:

    P[Y=y] = \binom{250}{y}0.06^y(0.94)^{250-y}\text{ for }y=0,1,2,3,\cdots,250

    We assume that each car has an equal probability of getting involved in an accents and accidents happen independently.

    e)
    \begin{aligned} P[Y\geq 3] &= 1-P[Y= 0]-P[Y= 1]-P[Y=2]\\ &=1-\binom{250}{0}0.06^0(0.94)^{250}-\binom{250}{1}0.06^1(0.94)^{249}-\binom{250}{2}0.06^2(0.94)^{248}\\ &=0.99997\\ &=99.997\% \end{aligned}

    f) i) We use the Binomial Distribution with parameters n=250 and p=0.06

    \begin{aligned} P[Y\lt 2] &= P[Y= 0]+P[Y= 1]\\ &=\binom{250}{0}0.06^0(0.94)^{250}+\binom{250}{1}0.06^1(0.94)^{249}\\ &=0.0000032458 \end{aligned}

    f) ii) Let us use the Poisson approximation to the Binomial Distribution.

    \begin{aligned} \lambda&=np\\ \lambda&=250\times 0.06\\ \lambda&=15 \end{aligned}

    \begin{aligned} P[Y\lt 2] &= P[Y= 0]+P[Y= 1]\\ &=\frac{15^0e^{-15}}{0!}+\frac{15^1e^{-15}}{1!}\\ &=0.0000048944 \end{aligned}

    The two probabilities are both very small and very close to each other indicating a good approximation.

    g) Consider the Binomial Distribution:

    \begin{aligned} E[Y] &= np\\ &=250\times 0.06\\ &=15 \end{aligned}

    \begin{aligned} Var[Y] &= np(1-p)\\ &=250\times 0.06 \times 0.94\\ &=14.1 \end{aligned}

    \begin{aligned} Var[Y] &= E[Y^2]-E[Y]^2\\ 14.1&=E[Y^2]-15^2\\ E[Y^2]&=14.1+15^2\\ E[Y^2]&=239.1 \end{aligned}

  • Year 2021 Question 4

    a)
    Number of Covid Cases Frequency
    10-20 6
    21-30 4
    31-40 9
    41-50 5
    51-60 6
    b) In order to work out part b), we must define the classes (and thus their boundaries) and their midpoint (a.k.a class mark):

    Number of Covid Cases Frequency (f_i) Class Midpoint (x_i)
    10-20 6 9.5\leq x \lt 20.5 15
    21-30 4 20.5\leq x \lt 30.5 25.5
    31-40 9 30.5\leq x \lt 40.5 35.5
    41-50 5 40.5\leq x \lt 50.5 45.5
    51-60 6 50.5\leq x \lt 60.5 55.5
    Note that the midpoint is calculated as the average of the class boundaries. For example the midpoint of the first class is \frac{9.5+20.5}{2}=15.

    i) The formula for calculating the mean of grouped data is given by:

    \begin{aligned} \bar{x}=\frac{\sum_{i=1}^N f_ix_i}{\sum_{i=1}^N f_i} \end{aligned}
    where N is the number of classes, f_i is the frequency of each class and x_i is the midpoint of each class.

    \begin{aligned} \bar{x}&=\frac{\sum_{i=1}^N f_ix_i}{\sum_{i=1}^N f_i}\\ &=\frac{6(15)+4(25.5)+9(35.5)+5(45.5)+6(55.5)}{6+4+9+5+6}\\ &=\frac{1072}{30}\\ &=35.7\dot{3} \end{aligned}

    ii) The formula for calculating the (sample) variance of grouped data is given by:

    \begin{aligned} s^2=\frac{1}{n-1}\sum_{i=1}^N f_i(x_i-\bar{x})^2 \end{aligned}
    where N is the number of classes, f_i is the frequency of each class, x_i is the midpoint of each class, and n is the sample size which is equal to the sum of frequencies \sum_{i=1}^N f_i.

    \begin{aligned} s^2&=\frac{1}{n-1}\sum_{i=1}^N f_i(x_i-\bar{x})^2\\ &=\frac{1}{30-1}[6(15-35.7\dot{3})^2+4(25.5-35.7\dot{3})^2+9(35.5-35.7\dot{3})^2+5(45.5-35.7\dot{3})^2+6(55.5-35.7\dot{3})^2]\\ &=\frac{1}{29}(5819.8\dot{6})\\ &=200.685 \end{aligned}

    iii) The standard deviation is the square root of the variance found in part ii).

    \begin{aligned} s&=\sqrt{200.685}\\ &=14.166 \end{aligned}

    iv) Let n be the sample size. In our case n=30. The median term is the:

    \begin{aligned} &\bigg(\frac{n+1}{2}\bigg)^{th}\text{ term}\\ =&\bigg(\frac{30+1}{2}\bigg)^{th}\text{ term}\\ =&15.5^{th}\text{ term} \end{aligned}

    The 15.5^{th} term lies in the class: 30.5\leq x \lt 40.5. Thus we shall call this class the median class.

    Let us use the formula of the median for grouped data in which:

    \begin{aligned} L_1&=30.5\text{ (lower boundary of the median class)}\\ n&=30 \text{ (sample size)}\\ \sum f &= 6+4=10 \text{ (sum of frequencies in classes lower than the median class)}\\ f_{median} &= 9\text{ (frequency of the median class)}\\ c &= 40.5-30.5=10\text{ (width of the median class)} \end{aligned}

    Hence by the formula:

    \begin{aligned} \text{Median}&=L_1+\bigg(\frac{\frac{n+1}{2}-\sum f}{f_{median}}\bigg) c\\ &=30.5+\bigg(\frac{\frac{30+1}{2}-10}{9}\bigg) 10\\ &=36.6\dot{1} \end{aligned}

    v) Let n be the sample size. In our case n=30. Quartle 1 is the 25^{th} percentile. Therefore Quartile 1 is the:

    \begin{aligned} &\bigg(\frac{25(n+1)}{100}\bigg)^{th}\text{ term}\\ =&\bigg(\frac{25(30+1)}{100}\bigg)^{th}\text{ term}\\ =&7.75^{th}\text{ term} \end{aligned}

    The 7.75^{th} term lies in the class: 20.5\leq x \lt 30.5. Thus we shall call this class the percentile class.

    Let us use the formula of the percentile for grouped data in which:

    \begin{aligned} L_1&=20.5\text{ (lower boundary of the percentile class)}\\ n&=30 \text{ (sample size)}\\ \sum f &= 6 \text{ (sum of frequencies in classes lower than the percentile class)}\\ f_{perc.} &= 4\text{ (frequency of the percentile class)}\\ c &= 30.5-20.5=10\text{ (width of the percentile class)} \end{aligned}

    Since Quartile 1 is the 25^{th} percentile, by the formula:

    \begin{aligned} r^{th}\text{ percentile}&=L_1+\bigg(\frac{\frac{r(n+1)}{100}-\sum f}{f_{perc.}}\bigg) c\\ \text{Quartile }1&=20.5+\bigg(\frac{\frac{25(30+1)}{100}-6}{4}\bigg) 10\\ &=24.875 \end{aligned}

    vi) Let n be the sample size. In our case n=30. Quartile 3 is the 75^{th} percentile. Therefore Quartile 3 is the:

    \begin{aligned} &\bigg(\frac{75(n+1)}{100}\bigg)^{th}\text{ term}\\ =&\bigg(\frac{75(30+1)}{100}\bigg)^{th}\text{ term}\\ =&23.25^{th}\text{ term} \end{aligned}

    The 23.25^{th} term lies in the class: 40.5\leq x \lt 50.5. Thus we shall call this class the percentile class.

    Let us use the formula of the percentile for grouped data in which:

    \begin{aligned} L_1&=40.5\text{ (lower boundary of the percentile class)}\\ n&=30 \text{ (sample size)}\\ \sum f &= 6+4+9=19 \text{ (sum of frequencies in classes lower than the percentile class)}\\ f_{perc.} &= 5\text{ (frequency of the percentile class)}\\ c &= 50.5-40.5=10\text{ (width of the percentile class)} \end{aligned}

    Since Quartile 3 is the 75^{th} percentile, by the formula:

    \begin{aligned} r^{th}\text{ percentile}&=L_1+\bigg(\frac{\frac{r(n+1)}{100}-\sum f}{f_{perc.}}\bigg) c\\ \text{Quartile }3&=40.5+\bigg(\frac{\frac{75(30+1)}{100}-19}{5}\bigg) 10\\ &=49 \end{aligned}

    vii) Let n be the sample size. In our case n=30. The 80^{th} percentile is the:

    \begin{aligned} &\bigg(\frac{80(n+1)}{100}\bigg)^{th}\text{ term}\\ =&\bigg(\frac{80(30+1)}{100}\bigg)^{th}\text{ term}\\ =&24.8^{th}\text{ term} \end{aligned}

    The 24.8^{th} term lies in the class: 50.5\leq x \lt 60.5. Thus we shall call this class the percentile class.

    Let us use the formula of the percentile for grouped data in which:

    \begin{aligned} L_1&=50.5\text{ (lower boundary of the percentile class)}\\ n&=30 \text{ (sample size)}\\ \sum f &= 6+4+9+5=24 \text{ (sum of frequencies in classes lower than the percentile class)}\\ f_{perc.} &= 6\text{ (frequency of the percentile class)}\\ c &= 60.5-50.5=10\text{ (width of the percentile class)} \end{aligned}

    By the formula:

    \begin{aligned} r^{th}\text{ percentile}&=L_1+\bigg(\frac{\frac{r(n+1)}{100}-\sum f}{f_{perc.}}\bigg) c\\ 80^{th}\text{ percentile}&=50.5+\bigg(\frac{\frac{80(30+1)}{100}-24}{6}\bigg) 10\\ &=51.8\dot{3} \end{aligned}

    f)
    \begin{aligned} \text{Skewness} &= \frac{3(\text{Mean}-\text{Median})}{\text{Standard Deviation}}\\ &=\frac{3(35.7\dot{3}-36.6\dot{1})}{14.166}\\ &=-0.186 \end{aligned}

  • Year 2021 Question 5

    a) Let S be the sample space. Therefore:

    S=\lbrace TTT,TTH,THT,HTT,HHT,HTH,THH,HHH \rbrace.

    Let A be the event that at least one head is obtained. Therefore:

    A=\lbrace TTH,THT,HTT,HHT,HTH,THH,HHH \rbrace.

    We have:

    \begin{aligned} P[A]&=\frac{\lvert A\rvert}{\lvert S \rvert}\\ &=\frac{7}{8}. \end{aligned}

    b) One way of finding such a probability is with the help of a tree diagram.


    \begin{aligned} &P[\text{\textquotedblleft first selection is green and second selection is red\textquotedblright}]\\ =&\frac{5}{12}\times\frac{7}{11}\\ =&\frac{35}{132}. \end{aligned}

    c) Note that the event "both diamonds" and the event "both kings" are mutually exclusive. Therefore:

    \begin{aligned} &P[\text{\textquotedblleft both diamonds or both kings\textquotedblright}]\\ =&P[\text{\textquotedblleft both diamonds\textquotedblright}]+P[\text{\textquotedblleft both kings\textquotedblright}]\\ =&\frac{\binom{13}{2}}{\binom{52}{2}}+\frac{\binom{4}{2}}{\binom{52}{2}}\\ =&\frac{14}{221}. \end{aligned}

    d) To work out

    e) Let S be the sample space. Therefore:

    S=\lbrace (1,1),(1,2),(1,3),\cdots,(6,6)\rbrace.

    Let A be the event that the total of the two dice is 10 or more. Therefore:

    A=\lbrace (4,6),(5,5),(5,6),(6,4),(6,5),(6,6)\rbrace.

    Let B be the event that the first die is a 5. Therefore:

    B=\lbrace (5,1),(5,2),(5,3),(5,4),(5,5),(5,6)\rbrace.

    \therefore P[B]=\frac{\lvert B\rvert}{\lvert S\rvert}=\frac{6}{36}

    We want to find P[A|B]. This will be done by using the formula for the conditional probability. First let us find the event A\cap B

    A\cap B=\lbrace (5,5),(5,6)\rbrace.

    \therefore P[A\cap B]=\frac{\lvert A\cap B\rvert}{\lvert S \rvert}=\frac{2}{36}

    By the conditional probability formula:

    \begin{aligned} P[A|B]&=\frac{P[A\cap B]}{P[B]}\\ &=\frac{\frac{2}{36}}{\frac{6}{36}}\\ &=\frac{2}{6}\\ &=\frac{1}{3}. \end{aligned}

    f)
    2\times P[A]=P[B]=\frac{5}{13}

    \begin{aligned} \therefore 2\times P[A]&=\frac{5}{13}\\ P[A]&=\frac{5}{26} \end{aligned} \begin{aligned} \qquad\qquad \end{aligned} \begin{aligned} P[B]=\frac{5}{13} \end{aligned}

    Let us find P[A\cap B]. By using the conditional probability formula:

    \begin{aligned} P[A|B]&=\frac{P[A\cap B]}{P[B]}\\ \frac{2}{5}&=\frac{P[A\cap B]}{\frac{5}{13}}\\ \frac{2}{5}\times\frac{5}{13}&=P[A\cap B]\\ P[A\cap B]&=\frac{2}{13} \end{aligned}

    Using the Inclusion-Exclusion formula:

    \begin{aligned} P[A\cup B]&=P[A]+P[B]-P[A\cap B]\\ &=\frac{5}{26}+\frac{5}{13}-\frac{2}{13}\\ &=\frac{11}{26}. \end{aligned}

    g) Two events A and B are independent if P[A\cap B]=P[A]P[B].

    Let us find P[A], P[B] and P[A\cap B]. Note that in this experiment (i.e. rolling a fair die once), the sample space S=\lbrace 1,2,3,4,5,6\rbrace.

    \begin{aligned} P[A]=\frac{\lvert A\rvert}{\lvert S \rvert}=\frac{1}{6} \end{aligned}

    \begin{aligned} P[B]=\frac{\lvert B\rvert}{\lvert S \rvert}=\frac{3}{6}=\frac{1}{2} \end{aligned}

    We have A\cap B=\lbrace 1\rbrace. Therefore:

    \begin{aligned} P[A\cap B]=\frac{\lvert A\cap B\rvert}{\lvert S \rvert}=\frac{1}{6} \end{aligned}

    So P[A\cap B]=\frac{1}{6}, but P[A]P[B]=\frac{1}{6}\times\frac{1}{2}=\frac{1}{12}. Therefore:

    P[A\cap B]\neq P[A]P[B]

    Hence A and B are not independent.

    h) Since A and B are mutually exclusive, A \cap B = \emptyset and thus P[A \cap B]=0.

    By the conditional probability formula:

    \begin{aligned} P[A|B]&=\frac{P[A\cap B]}{P[B]}\\ &=\frac{0}{0.9}\\ &=0. \end{aligned}

    Similarly,

    \begin{aligned} P[B|A]&=\frac{P[B\cap A]}{P[A]}\\ &=\frac{0}{0.9}\\ &=0. \end{aligned}

  • Year 2021 Question 6

    a) Consider the following 3 events.

    Let A be the event that the patient is diabetic.
    Let B be the event that the patient has high blood pressure.
    Let C be the event that the patient suffers from heart problems.

    Therefore: P[A]=0.4, P[B]=0.3 and P[C]=0.3.

    We also have: P[\text{\textquotedblleft Die\textquotedblright} | A]=0.2, P[\text{\textquotedblleft Die\textquotedblright} | B]=0.15 and P[\text{\textquotedblleft Die\textquotedblright} | C]=0.1.

    i) We want to find P[B|\text{\textquotedblleft Die\textquotedblright}]. Using Bayes' Formula:

    \begin{aligned} P[B|\text{\textquotedblleft Die\textquotedblright}]&=\frac{P[B]P[\text{\textquotedblleft Die\textquotedblright}|B]}{P[A]P[\text{\textquotedblleft Die\textquotedblright}|A]+P[B]P[\text{\textquotedblleft Die\textquotedblright}|B]+P[C]P[\text{\textquotedblleft Die\textquotedblright}|C]}\\ &=\frac{(0.3)(0.15)}{(0.4)(0.2)+(0.3)(0.15)+(0.3)(0.1)}\\ &=\frac{9}{31}. \end{aligned}

    ii) We want to find P[A|\text{\textquotedblleft Die\textquotedblright}]. Using Bayes' Formula:

    \begin{aligned} P[A|\text{\textquotedblleft Die\textquotedblright}]&=\frac{P[A]P[\text{\textquotedblleft Die\textquotedblright}|A]}{P[A]P[\text{\textquotedblleft Die\textquotedblright}|A]+P[B]P[\text{\textquotedblleft Die\textquotedblright}|B]+P[C]P[\text{\textquotedblleft Die\textquotedblright}|C]}\\ &=\frac{(0.4)(0.2)}{(0.4)(0.2)+(0.3)(0.15)+(0.3)(0.1)}\\ &=\frac{16}{31}. \end{aligned}

    iii) We want to find P[A|\text{\textquotedblleft Not Die\textquotedblright}]. Using Bayes' Formula:

    \begin{aligned} P[A|\text{\textquotedblleft Not Die\textquotedblright}]&=\frac{P[A]P[\text{\textquotedblleft Not Die\textquotedblright}|A]}{P[A]P[\text{\textquotedblleft Not Die\textquotedblright}|A]+P[B]P[\text{\textquotedblleft Not Die\textquotedblright}|B]+P[C]P[\text{\textquotedblleft Not Die\textquotedblright}|C]}\\ &=\frac{(0.4)(1-0.2)}{(0.4)(1-0.2)+(0.3)(1-0.15)+(0.3)(1-0.1)}\\ &=\frac{(0.4)(0.8)}{(0.4)(0.8)+(0.3)(0.85)+(0.3)(0.9)}\\ &=\frac{64}{169}. \end{aligned}

    b) i)
    ii)
    \begin{aligned} &P[\text{\textquotedblleft Wins at least once\textquotedblright}]\\ =&P[\text{\textquotedblleft Wins 1st game and Wins 2nd game\textquotedblright}]\\ &+P[\text{\textquotedblleft Wins 1st game and Losses 2nd game\textquotedblright}]\\ &+P[\text{\textquotedblleft Loses 1st game and Wins 2nd game\textquotedblright}]\\ =&(0.6)(0.6)+(0.6)(0.4)+(0.4)(0.6)\\ =&0.84 \end{aligned}

    iii)
    \begin{aligned} &P[\text{\textquotedblleft Wins both games\textquotedblright}]\\ =&P[\text{\textquotedblleft Wins 1st game and Wins 2nd game\textquotedblright}]\\ =&(0.6)(0.6)\\ =&0.36 \end{aligned}

  • Year 2020 Question 1


    Access the full catalogue of 3 years of detailed solutions to the past papers by clicking the login button below! Currently, the full catalogue is available to the students following my lessons as part of their course material. However if you are interested in accessing the solutions click the Register button below!

    Login
    Register

  • Year 2020 Question 2


    Access the full catalogue of 3 years of detailed solutions to the past papers by clicking the login button below! Currently, the full catalogue is available to the students following my lessons as part of their course material. However if you are interested in accessing the solutions click the Register button below!

    Login
    Register

  • Year 2020 Question 3


    Access the full catalogue of 3 years of detailed solutions to the past papers by clicking the login button below! Currently, the full catalogue is available to the students following my lessons as part of their course material. However if you are interested in accessing the solutions click the Register button below!

    Login
    Register

  • Year 2020 Question 4


    Access the full catalogue of 3 years of detailed solutions to the past papers by clicking the login button below! Currently, the full catalogue is available to the students following my lessons as part of their course material. However if you are interested in accessing the solutions click the Register button below!

    Login
    Register

  • Year 2020 Question 5


    Access the full catalogue of 3 years of detailed solutions to the past papers by clicking the login button below! Currently, the full catalogue is available to the students following my lessons as part of their course material. However if you are interested in accessing the solutions click the Register button below!

    Login
    Register

  • Year 2020 Question 6


    Access the full catalogue of 3 years of detailed solutions to the past papers by clicking the login button below! Currently, the full catalogue is available to the students following my lessons as part of their course material. However if you are interested in accessing the solutions click the Register button below!

    Login
    Register

  • Year 2019 Question 1


    Access the full catalogue of 3 years of detailed solutions to the past papers by clicking the login button below! Currently, the full catalogue is available to the students following my lessons as part of their course material. However if you are interested in accessing the solutions click the Register button below!

    Login
    Register

  • Year 2019 Question 2


    Access the full catalogue of 3 years of detailed solutions to the past papers by clicking the login button below! Currently, the full catalogue is available to the students following my lessons as part of their course material. However if you are interested in accessing the solutions click the Register button below!

    Login
    Register

  • Year 2019 Question 3


    Access the full catalogue of 3 years of detailed solutions to the past papers by clicking the login button below! Currently, the full catalogue is available to the students following my lessons as part of their course material. However if you are interested in accessing the solutions click the Register button below!

    Login
    Register

  • Year 2019 Question 4


    Access the full catalogue of 3 years of detailed solutions to the past papers by clicking the login button below! Currently, the full catalogue is available to the students following my lessons as part of their course material. However if you are interested in accessing the solutions click the Register button below!

    Login
    Register

  • Year 2019 Question 5


    Access the full catalogue of 3 years of detailed solutions to the past papers by clicking the login button below! Currently, the full catalogue is available to the students following my lessons as part of their course material. However if you are interested in accessing the solutions click the Register button below!

    Login
    Register

  • Year 2019 Question 6


    Access the full catalogue of 3 years of detailed solutions to the past papers by clicking the login button below! Currently, the full catalogue is available to the students following my lessons as part of their course material. However if you are interested in accessing the solutions click the Register button below!

    Login
    Register