MAT1115 - Introduction to Groups - Past Paper 2022 Solutions
The following are solutions to the 2022 Introduction to Groups exam questions for the study unit MAT1115 of the University of Malta B.Sc. Mathematics course.
Question 1
(a)
The order of a group (G,\cdot), denoted by o(G), is equal to the number of elements in the set G.
The order of an element g of the group (G,\cdot), denoted by o(g) is equal to the least positive integer m such that g^m=e.
(i)
Let G be a group and g \in G. Let the order of g be k (i.e. o(g)=k). Hence g^k=e.
The elements g,g^2,g^3,\cdots,g^k=e are in G (by closure in G).
Hence \lbrace g,g^2,g^3,\cdots,g^k=e\rbrace \subseteq G
Moreover this set is non-empty and closed, and hence it is a subgroup of G (by the finite subgroup test).
In fact, this subgroup is the cyclic group C_k.
It follows that:
\begin{aligned}o(C_k) &\mid o(G)\ (\text{by Lagrange's Theorem})\\k&\mid o(G)\\o(g)&\mid o(G)\ (\text{since }o(g)=k)\end{aligned}
\square
(ii)
By Lagrange’s Theorem, the order of a subgroup H divides the order of the group G. Hence the subgroups of a group of order p (where p is prime), must have order 1 or p.
The only subgroup of order 1 is H=\lbrace e\rbrace, since the identity is always an element of any group.
On the other hand, if H is a subgroup of G, and o(H)=o(G)=p, then H=G.
Hence the only subgroups of G are the trivial group \lbrace e\rbrace and the group G itself.
(b)
Let k\in F, where k is relatively prime to n.
Therefore, \exists a,b \in \mathbb{Z} such that:
\begin{aligned}ak+bn&=1\\ak&=1-bn\\ak&\equiv 1 \mod n\end{aligned}
Note that a is not a multiple of n since otherwise ak\equiv 0 \mod n.
Therefore:
\begin{aligned}a&=cn+z\ \exists z\in\lbrace 1,2,\cdots,n-1\rbrace\\\therefore ak&=cnk+zk\\ak\mod n &=cnk\mod n+zk\mod n\\1&\equiv zk \mod n\end{aligned}
\square
(c) (i)
A permutation on [n] is a bijective function f:[n]\rightarrow [n].
(ii)
The symmetric group of degree n, denoted by S_n is the group consisting of all the permutation on [n], with the binary operation defined by the composition of functions.
(d) (i)
The dihedral group D_n is the group of symmetries of a regular polygon on n edges (or n vertices). The dihedral group D_n has order n. If the vertices of the regular n-polygon are labelled 1,2,\cdots,n, then each symmetry in D_n is a permutation of [n]. Hence D_n is a subgroup of S_n, where o(S_n)=n!.
For n=3, o(D_3)=2(3)=6=3!=o(S_3). Hence S_3=D_3.
For n\neq 3, o(D_n)=2n\neq n!=o(S_n).
(ii)
Let D_3=\lbrace e,r,r^2,f,rf,r^2 f\rbrace where r is an anti-clockwise rotation of 120^o and f is a reflection (flip) in the vertical axis.
Let H=\lbrace e,f\rbrace.
H is a subgroup of D_3 because it is non-empty and closed since f^2=e (by the finite subgroup test). We have:
Hr=\lbrace r,fr\rbrace
and:
rH=\lbrace r,rf\rbrace
Since fr\neq rf, Hr\neq rH.
By the Theorem that states: Given a subgroup H of G, H\lhd G\text{ iff }Hg=gH\ \forall g\in G, then in our case H is not normal in D_3.
(iii)
By Lagrange’s Theorem, the subgroups of D_3 must have order 1,2,3 or 6.
The following are the normal subgroups of D_3:
\begin{aligned}K&=\lbrace e\rbrace\\K&=\lbrace e,r,r^2\rbrace\\K&=D_3\end{aligned}By the First Isomorphism Theorem, for a homomorphism \phi : G\rightarrow H with kernel K, we have \phi (G)\simeq G/K.
Hence when K=\lbrace e\rbrace, \phi (D_3)\simeq D_3; when K=\lbrace e,r,r^2\rbrace, \phi (D_3)\simeq D_3/\lbrace e,r,r^2\rbrace; and when K=D_3, \phi (D_3)\simeq D_3/D_3\simeq \lbrace e\rbrace.
Question 2
(a)
Let us show that \sim is reflexive, symmetric and transitive in \mathbb{Z}.
Reflexive?:
Let a\in\mathbb{Z}.
\begin{aligned}a&\equiv a\mod p\\\therefore a&\sim a\end{aligned}
Hence \sim is reflexive in \mathbb{Z}.
Symmetric?:
Let a,b\in\mathbb{Z} such that a\sim b.
\begin{aligned}\therefore a&\equiv b\mod p\\a&=kp+b\ \exists k \in\mathbb{Z}\\\therefore b&=a-kp\\b&=(-k)p+a\text{ where }-k\in\mathbb{Z}\\b&\equiv a\mod p\\\therefore b&\sim a\end{aligned}
Hence \sim is symmetric in \mathbb{Z}.
Transitive?:
Let a,b,c\in\mathbb{Z} such that a\sim b and b\sim c.
\therefore a\equiv b\mod p\text{ and }b\equiv c\mod p.
\therefore a=k_1 p+b\ \exists k_1\in\mathbb{Z}\text{ and }b=k_2 p+c\ \exists k_2\in\mathbb{Z}.
\begin{aligned}\therefore a&=k_1p+b\\&=k_1p+k_2p+c\\&=(k_1+k+2)p+c\text{ where }k_1+k_2\in\mathbb{Z}\\\therefore a &\equiv c\mod p\\\therefore a&\sim c\end{aligned}
Hence \sim is transitive in \mathbb{Z}.
Therefore the relation \sim is an equivalence relation on \mathbb{Z}.
\square
The distinct equivalence classes are: [0]=p\mathbb{Z},[1]=p\mathbb{Z}+1,\cdots,[p-1]=p\mathbb{Z}+(p-1).
Consider the set \lbrace [0],[1],\cdots,[p-1]\rbrace and binary operation +:
\begin{aligned}[0]+[1]&=[1]\\ [1]+[1]&=[2]\\ [2]+[1]&=[3]\\&\vdots\\ [p-1]+[1]&=[0]\end{aligned}
This is a group isomorphic to the cyclic group C_p.
(b)
Let us show that R is reflexive, symmetric and transitive in G.
Reflexive?:
Let c\in G:
\begin{aligned}&e\in H\text{ (since }H\text{ is a group and thus has the identity element)}\\ \therefore\ & cc^{-1}\in H\text{ (by inverse property of }G)\\\therefore\ & cRc\text{ (by definition of }R)\end{aligned}
Hence R is reflexive in G.
Symmetric?:
Let c,d\in G such that cRd:
\begin{aligned}\therefore\ & cd^{-1}\in H\text{ (by definition of }R)\\\therefore\ & (cd^{-1})^{-1}\in H\text{ (by inverse property)}\\\therefore\ &(d^{-1})^{-1}c^{-1}\in H\text{ (since }(ab)^{-1}=b^{-1}a^{-1}\ \forall a,b\in G)\\\therefore\ &dc^{-1}\in H\text{ (since}(a^{-1})^{-1}=a\ \forall a\in G)\\\therefore\ &dRc\text{ (by definition of }R)\end{aligned}
Hence R is symmetric in G.
Transitive?:
Let c,d,f\in G such that cRd and dRf:
\begin{aligned}\therefore\ & cd^{-1}\in H\text{ and } df^{-1}\in H\text{ (by definition of }R)\\\therefore\ &(cd^{-1})(df^{-1})\in H\text{ (by closure in }H)\\\therefore\ &c(d^{-1}d)f^{-1}\in H\text{ (by associativity in }H)\\\therefore\ &cef^{-1}\in H\text{ (by inverse in }H)\\\therefore\ &cf^{-1}\in H\text{ (by identity in }H)\\\therefore\ &cf^{-1}\in H\\\therefore\ &cRf\end{aligned}
Hence R is transitive in G. Hence R is an equivalence relationship.
Moreover:
\begin{aligned}[c]&=\lbrace d \in G:\ dRc\rbrace\\&=\lbrace d \in G:\ dc^{-1}\in H\rbrace\\&=\lbrace d \in G:\ dc^{-1}=h\ \exists h \in H\rbrace\\&=\lbrace d\in G:\ d=hc\ \exists h \in H\rbrace\\&=Hc\end{aligned}
This is the right coset of H in G by c. \square
(c) (i)
Let us show that g^{-1}Hg is a subgroup of G \forall g\in G.
Non-Emptiness?:
\begin{aligned}&H\text{ is a subgroup}\\\therefore\ & e \in H\text{ (by the identity property)}\\\therefore\ &g^{-1}eg\in g^{-1}Hg\\\therefore\ &g^{-1}Hg\neq\emptyset\end{aligned}
Hence g^{-1}Hg is non-empty.
Closure?:
Let g^{-1}h_1 g,g^{-1}h_2 g\in g^{-1}Hg.
\begin{aligned}&(g^{-1}h_1 g)(g^{-1}h_1 g)\\=&g^{-1}h_1 h_2 g\text{ (by associativity and inverse)}\\=&g^{-1}h_3 g\text{ (by closure in }H)\\ \in &g^{-1} Hg\end{aligned}
Hence closure holds. Hence g^{-1}H g is a subgroup of G \forall g\in G by the finite subgroup test. \square
(c) (ii)
Let f:H\rightarrow g^{-1}H g be a function defined by f(h)=g^{-1}hg\ \forall h \in H.
Let us show that f is a homomorphism and a bijective function.
Homomorphism?
Let h_1,h_2\in H:
\begin{aligned}f(h_1)f(h_2)&=(g^{-1}h_1 g)(g^{-1}h_2 g)\\&=g^{-1}h_1(gg^{-1})h_2 g\text{ (by associativity)}\\&=g^{-1}h_1h_2 g\text{ (by inverse and identity)}\\&=f(h_1 h_2)\end{aligned}
Hence f is a homomorphism.
One-to-One?
Let h_1,h_2\in H such that f(h_1)=f(h_2).
\begin{aligned}\therefore\ g^{-1}h_1 g&=g^{-1}h_2 g\\h_1&=h_2\text{ (by associativity, inverse and identity)}\end{aligned}
Hence f is one-to-one.
Onto?
Let g^{-1}hg\in g^{-1}Hg such that f(h_1)=f(h_2).
Therefore h \in H such that f(h)=g^{-1}hg.
Hence f is onto.
Hence H and g^{-1}Hg are isomorphic. \square
(iii)
Let us show that H\lhd G.
Both H and g^{-1}Hg are subgroups of G (by Part (i)).
Moreover H\simeq g^{-1}Hg (by Part (ii)).
Therefore o(H)=o(g^{-1}Hg)=r.
Since G has exactly one subgroup of order r, then:
\begin{aligned}H&=g^{-1}Hg\\\therefore\ H&\subseteq g^{-1}Hg\ \forall g \in G\\\therefore\ H\lhd G\text{ (by definition of normal subgroup)}\end{aligned}
\square
(d)
The divisors of 36 are: 1,2,3,4,6,9,12,18,36.
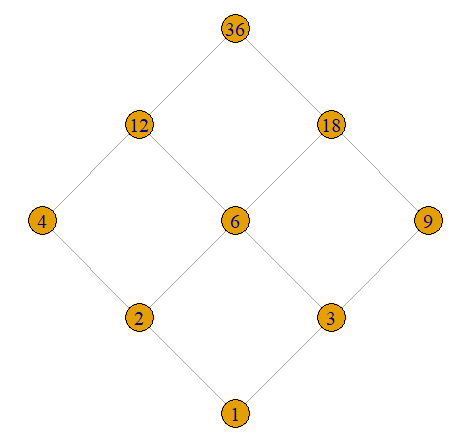
We have \sup(12,18)=36 and \inf(12,18)=6.
Note that the \sup(a,b) is a number c on the lowest level possible which has a path connecting it to a and a path connecting it to b. On the other hand, the \inf(a,b) is a number c on the highest level possible which has a path connecting it to a and a path connecting it to b.
Question 3
(a) (i)
Let ab\equiv 0\mod 15\ \exists b\in F_{15}. Suppose for contradiction that a has an inverse in (F_{15},\times).
Hence ax\equiv 1 \mod 15\ \exists x \in F_{15}.
Note that since ab\equiv 0\mod 15 and ax\equiv 1\mod 15, then x \neq b.
Since ax\equiv 1\mod 15 and ab\equiv 0\mod 15:
\begin{aligned}ax-ab&\equiv 1 \mod 15\\a(x-b)&\equiv 1 \mod 15\end{aligned}
Case 1: x>b
Therefore x-b\in F_{15} where x-b is also an inverse of a. This is a contradiction since the inverse must be unique.
Case 2: x<b
\begin{aligned}a(x-b)&\equiv 1 \mod 15\\a(x-b)+15a&\equiv 1 \mod 15\\a(x-b+15)&\equiv 1 \mod 15\end{aligned}
Therefore x-b+15\in F_{15} where x-b+15 is also an inverse of a. This is a contradiction since the inverse must be unique. Hence the result follows. \square
(ii)
3\times 5=15\equiv 0 \mod 15. Hence 3 and 5 do not have an inverse under multiplication modulo 15.
6\times 5=30\equiv 0 \mod 15. Hence 6 does not have an inverse under multiplication modulo 15.
9\times 5=45\equiv 0 \mod 15. Hence 9 does not have an inverse under multiplication modulo 15.
10\times 3=30\equiv 0 \mod 15. Hence 10 does not have an inverse under multiplication modulo 15.
12\times 5=60\equiv 0 \mod 15. Hence 12 does not have an inverse under multiplication modulo 15.
Hence 3, 5, 6, 9, 10, 12 do not have an inverse under multiplication modulo 15.
(iii)
The Residue Group R_{15} is a group made up of the integers from \lbrace 1,2,\cdots,14\rbrace that are relatively prime to 15, together with the binary operation \times_{15}. Hence R_{15}=\lbrace 1,2,4,7,8,11,13,14\rbrace, which has order 8.
(b)
Let us show that x^k generates C_n if and only if k and n are coprime.
\begin{aligned}&\gcd (k,n)=1\\\Leftrightarrow&\exists a,b\in\mathbb{Z}:ak+bn=1\\\Leftrightarrow&x=x^1=x^{ak+bn}=x^{ak}x^{bn}=x^{ak}=(x^k)^a\\\Leftrightarrow & C_n=<x>=<x^k>\end{aligned}
The number of integers from 1 to n-1, that are coprime to n is equal to \phi(n). Hence there are \phi(n) generators for C_n. In particular there are \phi(15) generators for C_{15}. \square
(c)
(d) (i)
Let g\in G, where G is a finite group. Let us show that o(g)=o(g^{-1}).
Let k=o(g). Therefore g^k=e and g^m\neq e for m\in\mathbb{Z}^{+},m<k
\begin{aligned}g^{-k}g^k&=e\text{ by associativity, inverse and identity)}\\g^{-k}e&=e\text{ (since }g^k=e)\\g^k&=e\text{ (by identity)}\\\therefore \ (g^{-1})^k&=e\end{aligned}
Suppose that g^{-m}=e for some m\in\mathbb{Z}^{+},m<k.
\begin{aligned}g^m g^{-m}&=e\text{ by associativity, inverse and identity)}\\g^{m}e&=e\text{ (since }g^{-m}=e)\\g^m&=e\text{ (by identity)}\\\therefore \ (g^{-1})^m=e\end{aligned}
This contradicts the fact that o(g)=k.
Hence it follows that o(g^{-1})=o(g)=k \square
(ii)
Note that for an element g of order 2 (g^2=e), we have g=g^{-1}. The elements of G follows one and only one of the following 3 cases:
(a) g=e
(b) g\neq e and g=g^{-1} (i.e. the elements of order 2)
(c) g\neq e and g\neq g^{-1}
Let S_1 be the set of elements of G following case (a).
Let S_2 be the set of elements of G following case (b).
Let S_3 be the set of elements of G following case (c).
We have \lvert S_1\rvert since it contains the identity element and the identity element is unique. Moreover, \lvert S_3\rvert is even since for all g\in S_3, g^{-1}\in S_3 because (g^{-1})^{-1}=g and g^{-1}\neq g.
We have:
\begin{aligned}\lvert G\rvert &=\lvert S_1\rvert+\lvert S_2\rvert+\lvert S_3\rvert\\&=1+0+2m\ \exists m\in\mathbb{Z}\\&=2m+1\end{aligned}
Hence G has an odd number of elements. \square
Question 4
(a)
Let G be an abelian group and let H be a subgroup of G.
Let g \in G:
\begin{aligned}\forall h \in H\ g^{-1}hg &=g^{-1}g h\text{ (since }G\text{ is abelian)}\\&=h\end{aligned}
Hence g^{-1}Hg=H\ \forall g \in G and in particular g^{-1}Hg\subseteq H\ \forall g \in G . \square
(b) (i)
Let \phi :G\rightarrow H be a homomorphism with kernel K. Let us prove that \phi (G)\simeq G /K. Thus for every homomorphism with kernel K, the image is always isomorphic to the factor group generated by the kernel, implying that the homomorphic image of G with kernel K is unique.
Consider a mapping: \psi : G/K \rightarrow \phi (G) defined by \psi (K g)=\phi(g)\ \forall g\in G.
r.t.p.:
a) \psi is well-defined;
b) \psi is a homomorphism;
c) \psi is a bijection (\therefore isomorphism).
a) Let Kg_1=Kg_2 where g_1,g_2\in G, r.t.p. \psi (Kg_1)=\psi (Kg_2).
Since Kg_1=Kg_2, then there exists k_1,k_2\in K:\ k_1 g_1=k_2 g_2. Therefore: g_1=k_1^{-1}k_2g_2.
\begin{aligned}\psi (Kg_1)&=\phi(g_1)\text{ (by definition of }\psi)\\&=\phi (k_1^{-1}k_2g_2)\text{ (since }g_1=k_1^{-1}k_2g_2)\\&=\phi (k_1^{-1}k_2)\phi(g_2)\text{ (since }\phi\text{ is a homomorphism)}\\&=\phi(g_2)\text{ (since }K\text{ is the kernel which is a subgroup)}\\&=\psi(Kg_2)\text{ (by definition of }\psi)\end{aligned}
Hence \psi is well-defined.
b) Let g_1,g_2\in G:
\begin{aligned}\psi (Kg_1 Kg_2)&=\psi (Kg_1 g_2)\text{ (since }K\text{ is normal in }G)\\&=\phi(g_1 g_2)\text{ (by definition of }\psi)\\&=\phi(g_1)\phi(g_2)\text{ (since }\phi\text{ is a homomorphism)}\\&=\psi(Kg_1)\psi(Kg_2)\end{aligned}
Hence \psi is a homomorphism.
c) One-to-One?: Let \psi (Kg_1)=\psi (Kg_2). R.t.p. Kg_1=Kg_2.
\begin{aligned}\psi (Kg_1)&=\psi (Kg_2)\\\therefore\ \phi (g_1)&=\phi (g_2)\text{ (by definition of }\psi)\\\phi (g_1)\phi(g_2)^{-1}&=e_2\text{ (where }e_2\text{ is the identity of }H)\\\phi (g_1)\phi (g_2^{-1})&=e_2\text{ (since for a homomorphism }\phi,\ \phi(g)^{-1}=\phi(g^{-1}))\\\phi(g_1g_2^{-1})&=e_2\text{ (since }\phi\text{ is a homomorphism)}\\\therefore\ g_1 g_2^{-1}&\in K\\\therefore\ g_2 g_1^{-1}&\in K\text{ (by inverses, since }K\text{ is a subgroup of }G)\end{aligned}
Let k_1g_1\in Kg_1:
\begin{aligned}k_1g_1&=k_1g_1g_2^{-1}g_2\\&=(k_1g_1g_2^{-1})g_2\\&\in K g_2\end{aligned}
Let k_2g_2\in Kg_2:
\begin{aligned}k_2g_2&=k_2g_2g_1^{-1}g_1\\&=(k_2g_2g_1^{-1})g_1\\&\in K g_1\end{aligned}
Hence Kg_1=Kg_2 and thus \psi is one-to-one.
Onto?: Let \phi(g)\in\phi(G).
There exists Kg\in G/K. We have \psi(Kg)=\phi(g), by definition of \psi. Hence \psi is onto.
Hence \phi (G)\simeq G/K. \square
(b) (ii)
By the Lagrange’s Theorem, we know that the cosets of a subgroup partition the group and the cardinalities of the cosets (and the subgroup) are all equal. Moreover since o(K)=\frac{1}{2}o(G), and K is a subgroup of G, we have G/K=\lbrace K,Kg\rbrace, where g\in G but g\notin K.
Hence by the Isomorphism Theorem, \phi (G)\simeq \lbrace K,Kg\rbrace and \lbrace K,Kg\rbrace \simeq C_2, since we know that there exists only one group with two elements, namely the cyclic group of order 2.
(c)
(d)
Let us prove the following in this order (i)\Rightarrow(ii), (ii)\Rightarrow(iii), (iii)\Rightarrow(iv) and (iv)\Rightarrow(i).
(i)\Rightarrow (ii):
Let N be a normal subgroup of G. Hence \forall g \in G: g^{-1}Ng \subseteq N. Let us prove that \forall g \in G: N\subseteq g^{-1}Ng.
Let n\in N:
\begin{aligned}n&=ene\\&=(g^{-1}g)n(g^{-1}g)\text{ (for any }g\in G)\\&=g^{-1}(gng^{-1})g\text{ (by associativity)}\\&=g^{-1}((g^{-1})^{-1}n^{-1}g^{-1})^{-1}g\end{aligned}
Since g^{-1}\in G and n^{-1}\in N, we have (g^{-1})^{-1}n^{-1}g^{-1}\in (g^{-1})^{-1}Ng^{-1}\subseteq N (since N is normal).
Hence (g^{-1})^{-1}n^{-1}g^{-1}=n' for some n'\in N.
\begin{aligned}n&=g^{-1}{n'}^{-1}g\\&\in g^{-1}Ng\end{aligned}
(ii)\Rightarrow (iii): Let ng\in Ng:
\begin{aligned}ng&=(gg^{-1})ng\\&=g(g^{-1}ng)\\&=gn'\ (\exists n'\in N,\text{ since }g^{-1}Ng=N\ \forall g\in G)\\&\in gN\end{aligned}
Let gn\in gN:
\begin{aligned}gn&=gn(g^{-1}g)\\&=(gng^{-1})g\\&=((g^{-1})^{-1}ng^{-1})g\\&=n'g\ (\exists n'\in N,\text{ since }g^{-1}Ng=N\ \forall g\in G)\\&\in Ng\end{aligned}
Hence gN=Ng\ \forall g\in G.
(iii)\Rightarrow (iv): Let n_1a n_2b\in NaNb:
\begin{aligned}&n_1 a n_2 b\\=&n_1 n_3ab\ (\exists n_3\in N,\text{ since }Ng=gN\ \forall g\in G)\\\in& Nab\end{aligned}
Let nab\in Nab:
\begin{aligned}&nab\\=&naeb\\\in& NaNb\end{aligned}
Hence NaNb=Nab\ \forall a,b\in G.
(iv)\Rightarrow (i): Let g^{-1}ng\in g^{-1}Ng.
\begin{aligned}g^{-1}ng&=eg^{-1}ng\\&=n'g^{-1}g\ (\exists n'\in N, \text{ since }NaNb=Nab\ \forall a,b\in G)\\&=n'e\\&=n'\\&\in N\end{aligned}
(e)
Let Ng\in G/N:
\begin{aligned}NgNe&=Nge\\&=Ng\end{aligned}
Similarly:
\begin{aligned}NeNg&=Neg\\&=Ng\end{aligned}
Hence Ne is the identity element of G/N.
\begin{aligned}NgNg^{-1}&=Ngg^{-1}\\&=Ne\end{aligned}
Similarly:
\begin{aligned}Ng^{-1}Ng&=Ng^{-1}g\\&=Ne\end{aligned}
Hence Ng^{-1} is the inverse element of Ng in G/N.