Plotting Quadratic Equations

These topics are covered in the Mathematics syllabus in preparation for the University of Malta MATSEC O level exam. However a strong knowledge of such topics will prove to be extremely important and useful for the workings in the A level topics. These topics are intended as a revision and brush-up for students starting their A level Pure Mathematics in Malta.

Quadratic equations have the following form:

y=ax^2+bx+c

where a,b and c are some numbers. However a must not be zero (a\neq 0). In fact, if a where 0, the equation above becomes y=bx+c which is the equation of a straight line and not a quadratic. The following are examples of quadratic equations:

\begin{aligned}(1)& \ y=x^2+3x-1\\(2)&\ y=3x^2+1\\(3)& \ y=-x^2+x\\(4)& \ y=(x-1)^2\end{aligned}

In quadratic (1), we have a=1, b=3 and c=-1. In quadratic (2), we note that the term in x is missing (i.e. b=0). Still this is a quadratic equation because the term in x^2 is present. Similarly in quadratic (3), the constant term is missing (i.e. c=0). Still this remains a quadratic equation because the term in x^2 is present. Finally, quadratic (4) is a quadratic because when we expand (open up) the brackets we obtain y=x^2-2x+1 and this has the term in x^2 present.

The two different shapes of the quadratic equation

There are two different shapes that a quadratic equation can take, when plotted. The first shape is the U-shape where the quadratic has the shape of the letter “U” and the second shape is the N-shape where the quadratic has the shape of the letter “n”. The shape of the quadratic equation y=ax^2+bx+c is determine only by the coefficient of x^2. If a>0, the quadratic is U-shaped. If a<0, the quadratic is N-shaped. The following diagram helps you remember this rule.

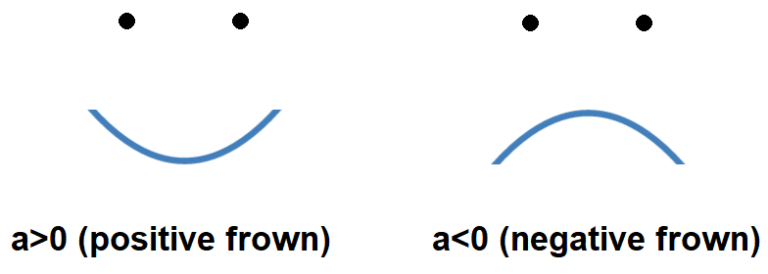
Shape of Quadratics

Example: Determine the shape of the following quadratics:

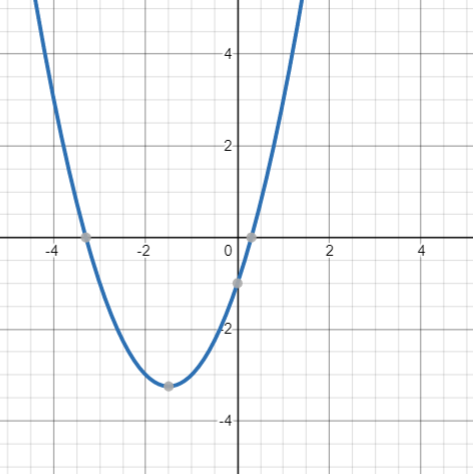
(a) y=x^2+3x-1

We have a=1, thus a>0. So the quadratic is U-shaped. In fact the plot of this quadratic is the following:

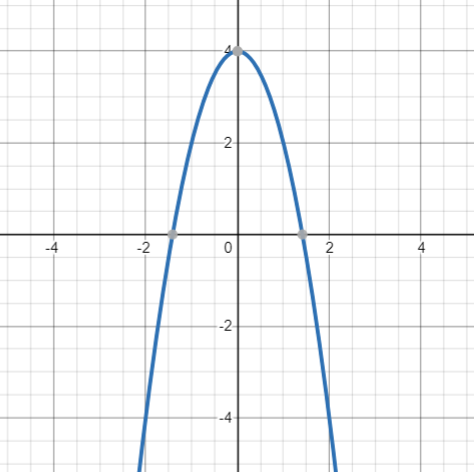
(b) y=-2x^2+4

We have a=-2, thus a<0. So the quadratic is N-shaped. In fact the plot of this quadratic is the following:

(c) y=(x-1)^2

Let us expand this quadratic equation:

\begin{aligned}y&=(x-1)^2\\y&=(x-1)(x-1)\\y&=x^2-2x+1\\ & \end{aligned}

We have a=1, thus a>0. So the quadratic is U-shaped. In fact the plot of this quadratic is the following:

(b) y=-(x+1)^2

Let us expand this quadratic equation:

\begin{aligned}y&=-(x+1)^2\\y&=-(x+1)(x+1)\\y&=-(x^2+2x+1)\\y&=-x^2-2x-1\end{aligned}

We have a=-1, thus a<0. So the quadratic is N-shaped. In fact the plot of this quadratic is the following:

Plotting Quadratic Equations

We will plot quadratic equations by using just 3 steps as follows:

Step 1: We find the x-intercept(s) (also known as the root(s)). This is done by letting y=0 in the equation, factorising the quadratic and solving for x.

Step 2: We find the y-intercept (the point where the graph crosses the y-axis). This is done by letting x=0 in the equation and solving for y.

Step 3: We check whether the curve is U-shaped or N-shaped and draw a curved line through the x-intercept(s) and the y-intercept. Note that the graph reaches its minimum/maximum point exactly between the roots.

A note regarding the x-intercept(s): We will have either two different x-intercepts, or just one distinct x-intercept or else no x-intercepts. The case where we have no x-intercepts will be discussed in more details in the A-level topic on Differentiation.

Example 1: Plot the following equation: y=x^2+2x-3

In Step 1, let y=0,

\begin{aligned}0&=x^2+2x-3\\0&=(x+3)(x-1) \end{aligned}
\begin{aligned} x+3&= 0  &  x-1& = 0\\x&=-3 & x&=1\end{aligned}

Therefore the roots are (-3,0) and (1,0)

In Step 2, we let x=0,

\begin{aligned}y&=0^2+2(0)-3\\y&=-3 \end{aligned}

Therefore the y-intercept is (0,-3). We draw a curve through the roots and the y-intercept that is symmetric between the roots. Note that since a>0, the curve will be U-shaped.

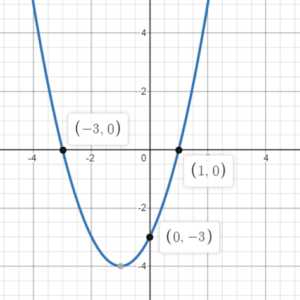
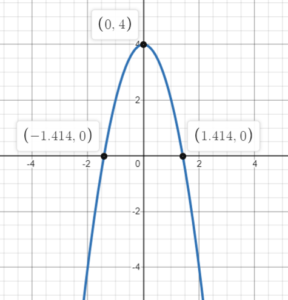
Example 2: Plot the following equation: y=-2x^2+4

In Step 1, let y=0,

\begin{aligned}0&=-2x^2+4\\0&=x^2-2 \text{ (divide both sides by }-2 )\\0&=(x+\sqrt{2})(x-\sqrt{2})\end{aligned}
\begin{aligned} x+\sqrt{2}&= 0  &  x-\sqrt{2}& = 0\\x&=-\sqrt{2} & x&=\sqrt{2}\end{aligned}

Therefore the roots are (-\sqrt{2},0) and (\sqrt{2},0)

In Step 2, we let x=0,

\begin{aligned}y&=-2(0^2)+4\\y&=4 \end{aligned}

Therefore the y-intercept is (0,4). We draw a curve through the roots and the y-intercept that is symmetric between the roots. Note that in this example, a=-2>0, hence the curve will be N-shaped.

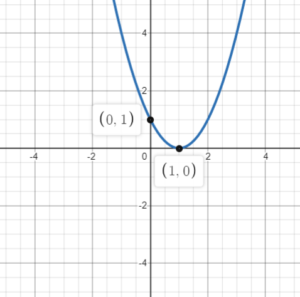
Example 3: Plot the following equation: y=(x-1)^2

In Step 1, let y=0,

\begin{aligned}0&=(x-1)^2\\0&=(x-1)(x-1)\end{aligned}
\begin{aligned} x-1&= 0  &  x-1& = 0\\x&=1 & x&=1\end{aligned}

Note that here we have just one distinct root (in other words, a repeated root) which is given by the coordinates (1,0).

In Step 2, we let x=0,

\begin{aligned}y&=(0-1)^2\\y&= (-1)^2\\y&=1\end{aligned}

Therefore the y-intercept is (0,1).

For Step 3, let us expand the quadratic in order to determine its shape.

\begin{aligned}y&=(x-1)^2\\y&=(x-1)(x-1)\\y&=x^2-2x+1\end{aligned}

Since a=1>0, the curve will be U-shaped. We draw a U-shaped curve passing through the root and the y-intercept.

Summary

We have learnt how to plot a quadratic equation in 3 simple steps. In Step 1, we find the x-intercepts (roots), in Step 2, we find the y-intercept and finally in Step 3, we determine the shape of the quadratic (U-shape or N-shape) and plot the curve.

Note that in the case of a quadratic equation that has no roots (no x-intercepts), we need to find the minimum or maximum point in order to be able to get a decent plot. However this case will be covered in the topic of Differentiation.

Exercises

Plot the following quadratic equations:

a) y=x^2-x

b) y=4-x^2

c) y=x^2

d) y=x^2+4x+4

e) y=2x^2-2x+\frac{1}{2}

f) y=2(x+1)(x+4)