Plotting Straight Lines

These topics are covered in the Mathematics syllabus in preparation for the University of Malta MATSEC O level exam. However a strong knowledge of such topics will prove to be extremely important and useful for the workings in the A level topics. These topics are intended as a revision and brush-up for students starting their A level Pure Mathematics in Malta.

The equation of the straight line is given by the formula:

$y=ax+b$ for some numbers $a$ and $b$ .

The following are examples of straights lines:

\begin{aligned}(1)& \ y=3x-1\\(2)&\ y=-x+2\\(3)& \ y=2x\\(4)& \ y=2\end{aligned}

Line (3) results when the value of $b$ is $0$ . In fact the equation could have been written as $y=2x+0$ . Line (4) results when the value of $a$ is $0$ . In fact the equation could have been written as $y=0x+2$ .

In what follows we consider four cases of the straight line and learn how to plot the straight line in each case.

Case 1: $y=ax+b$ where $a \neq 0$ and $b \neq 0$

We plot this line in 3 steps:

Step 1: We let $y=0$ in order to find the $x$ -intercept (the root), which is the point where the line crosses the $x$ -axis.

Step 2: We let $x=0$ in order to find the $y$ -intercept, which is the point where the line crosses the $y$ -axis.

Step 3: Then we draw the line passing through the $x$ -intercept (the root) and the $y$ -intercept.

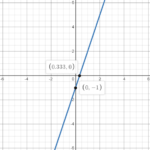
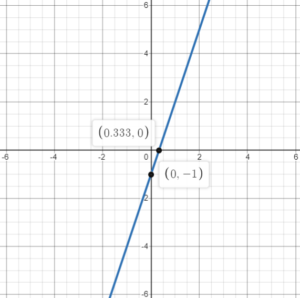
Example 1: Plot the line $y=3x-1$

In Step 1, let $x=0$ in the equation of the line:

\begin{aligned}y&=3(0)-1\\y&=-1\end{aligned}

We obtain the point $(0,-1)$ .

In Step 2, let $y=0$ in the equation of the line and make $x$ subject of the formula:

\begin{aligned}0&=3x-1\\1&=3x\\3x&=1\\x&=\frac{1}{3}\end{aligned}

We obtain the point $(\frac{1}{3},0)$ .

In Step 3, we take the points $(0,-1)$ and $(\frac{1}{3},0)$ , plot them and draw a line through them.

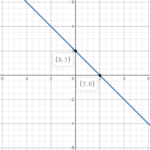
Example 2: Plot the line $y=-x+2$

In Step 1, let $x=0$ in the equation of the line:

\begin{aligned}y&=-0+2\\y&=2\end{aligned}

We obtain the point $(0,2)$ .

In Step 2, let $y=0$ in the equation of the line and make $x$ subject of the formula:

\begin{aligned}0&=-x+2\\x&=2\end{aligned}

We obtain the point $(2,0)$ .

In Step 3, we take the points $(0,2)$ and $(2,0)$ , plot them and draw a line through them.

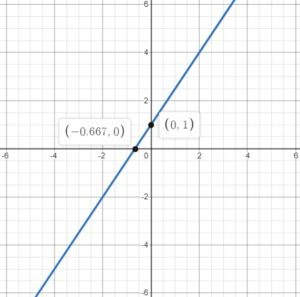
Example 3: Plot the line $2y=3x+2$

Although here the coefficient of $y$ is not 1 (equal to 2 in this example), we still carry out the usual three steps in order to plot this line. In Step 1, let $x=0$ and make $y$ subject of the formula:

\begin{aligned}2y&=3(0)+2\\2y&=2\\y&=1\end{aligned}

We obtain the point $(0,1)$ .

In Step 2, let $y=0$ in the equation of the line and make $x$ subject of the formula:

\begin{aligned}2(0)&=3x+2\\0&=3x+2\\-3x&=2\\x&=-\frac{2}{3}\end{aligned}

We obtain the point $(-\frac{2}{3},0)$ .

In Step 3, we take the points $(0,1)$ and $(-\frac{2}{3},0)$ , plot them and draw a line through them.

Case 2: $y=ax$ where $a \neq 0$

In this case, there is no constant term in the equation of the line. We do have a term in $x$ and a term in $y$ but the constant term is missing. This line always passes from the origin $(0,0)$ , because if you put $x=0$ in the equation, you always get $y=0$ . So we already know one point that lies on the line. We plot this line in 2 steps:

Step 1: We let $x$ be some non-zero value, for example $x=1$ and find the corresponding value of $y$ .

Step 2: Then we draw the line passing through the origin $(0,0)$ and the point found in Step 1.

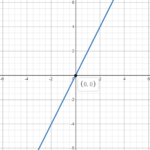
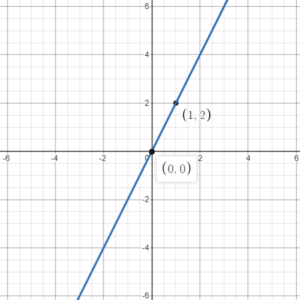
Example 1: Plot the line $y=2x$

Notice that in the equation of this line, there is no constant term. We just have a term in $x$ and a term in $y$ . So the origin $(0,0)$ lies on the line. In Step 1, let $x=1$ and make $y$ subject of the formula:

\begin{aligned}y&=2(1)\\y&=2\end{aligned}

We obtain the point $(1,2)$ .

In Step 3, we take the points $(0,0)$ and $(1,2)$ , plot them and draw a line through them.

Example 2: Plot the line $-4y=2x$

Notice that in the equation of this line, again there is no constant term. So we are dealing with the Case 2. So the origin $(0,0)$ lies on the line. In Step 1, let $x=1$ and make $y$ subject of the formula:

\begin{aligned}-4y&=2(1)\\-4y&=2\\y&=-\frac{1}{2}\end{aligned}

We obtain the point $(1,-\frac{1}{2})$ .

In Step 3, we take the points $(0,0)$ and $(1,-\frac{1}{2})$ , plot them and draw a line through them.

Case 3: $y=b$ for some number $b$

For any value of $x$ , y is always equal to $b$ . Hence this gives us a horizontal line with $y$ -intercept equal to $b$ . Another way to look at this is that we are after the all the points in the $xy$ -plane whose $y$ -value is equal to $b$ . Again, this gives us a horizontal line with $y$ -intercept equal to $b$ .

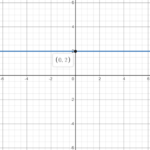
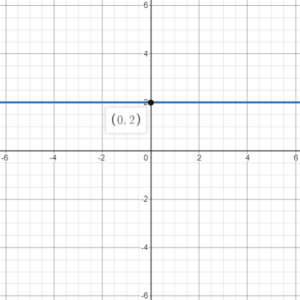
Example 1: Plot the line $y=2$

Here we just plot a horizontal line with $y$ -intercept equal to $2$ .

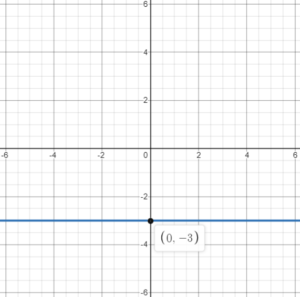
Example 2: Plot the line $y=-3$

Here we just plot a horizontal line with $y$ -intercept equal to $-3$ .

Case 4: $x=c$ for some number $c$

Here we are after all the points in the $xy$ -plane whose $x$ -value is equal to $c$ . This gives us a vertical line with $x$ -intercept equal to $c$ .

Example 1: Plot the line $x=-1$

We plot a horizontal line with $x$ -intercept equal to $-1$ .

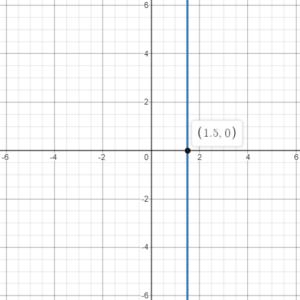
Example 2: Plot the line $x=\frac{3}{2}$

We plot a horizontal line with $x$ -intercept equal to $\frac{3}{2}$ .

Summary

We have learnt how to draw a straight line in four different case. In Case 1, we had the general straight line equation $y=ax+b$ . In Case 2, we had lines with no constant term, that is, of the form $y=ax$ . In Case 3, we considered lines of the form $y=b$ for some number $b$ and these are simply horizontal lines. In Case 4, we considered lines of the form $x=c$ for some number $c$ and these are simply vertical lines.

Exercises

Plot the following lines:

a) $y=4x+2$

b) $y-3x=2$

c) $x+2y+1=0$

d) $y=\frac{1}{2}x$

e) $2x-3y=0$

f) $y=\frac{1}{3}$

g) $y=0$

h) $x=-2$

i) $x=0$