Surds

Matsec Syllabus: Pure Mathematics Paper 1 Topic 1: Use and manipulation of surds: To include simplification and rationalisation of the denominator of a fraction e.g. \sqrt{15}-4\sqrt{27}; \frac{3\sqrt{2}-2\sqrt{3}}{4\sqrt{2}-3\sqrt{3}}.

Introduction

Surds are numbers of the form \sqrt{p} where p is a positive integer, but NOT a square number.

Examples of Surds:

(a) \sqrt{2}

(b) \sqrt{3}

(c) \sqrt{5}

(d) \sqrt{6}

Note that surds cannot be expressed as a fraction of two whole numbers (integers) and therefore surds are examples of irrational number. Refer to Types Of Numbers.

Note that \sqrt{4} is NOT a surd because 4 is a square number and thus \sqrt{4} simplifies as follows:

\begin{aligned}\sqrt{4}=\sqrt{2^2}=2\end{aligned}.

Note that by definition of the squared function and square root function, these two function cancel each other out, as follows:

\boxed{\sqrt{a^2}=a} and \boxed{(\sqrt{a})^2=a}

Three Rules of Surds

We have only the following three rules of surds which you must remember. Let a and b be any two numbers.

Rule 1:

\boxed{\sqrt{ab}=\sqrt{a}\sqrt{b}}

Rule 2:

\boxed{\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}}

In Rule 1, if we have a product inside a square root, we split the square root by making a square root with both factors. In Rule 2, if we have a fraction inside a square root, we split the square root by making a square root with both the numerator and the denominator.

From Rule 1, when a=b, it follows that:

\begin{aligned}\sqrt{aa}&=\sqrt{a}\sqrt{a}\\\sqrt{a^2}&=\sqrt{a}\sqrt{a}\\a&=\sqrt{a}\sqrt{a}\text{  (since the square root and the squared cancel each other out)}\end{aligned}

Let us call this Rule 3.

Rule 3:

\boxed{\sqrt{a}\sqrt{a}=a}

Simplifying Surds

We are going to use the first 2 rules in order to simplify surds. In simplifying surds, we would like to have a smaller number inside the square root. This is achieved by expressing the number inside the square root as a product of two factors, one of which is a square number.

Example 1: Simplify the following surds:

(a) \sqrt{12}

\begin{aligned}&\sqrt{12}\\=&\sqrt{4\times3}\\=&\sqrt{4}\sqrt{3}\text{ (by Rule 1)}\\=&2\sqrt{3}\end{aligned}

(b) \sqrt{8}

\begin{aligned}&\sqrt{8}\\=&\sqrt{4\times 2}\\=&\sqrt{4}\sqrt{2}\text{ (by Rule 1)}\\=&2\sqrt{2}\end{aligned}

(c) \sqrt{45}

\begin{aligned}&\sqrt{45}\\=&\sqrt{9\times 5}\\=&\sqrt{9}\sqrt{5}\text{ (by Rule 1)}\\=&3\sqrt{5}\end{aligned}

(d) \sqrt{700}

\begin{aligned}&\sqrt{700}\\=&\sqrt{100\times 7}\\=&\sqrt{100}\sqrt{7}\text{ (by Rule 1)}\\=&10\sqrt{7}\end{aligned}

(e) \sqrt{\frac{4}{9}}

\begin{aligned}&\sqrt{\frac{4}{9}}\\=&\frac{\sqrt{4}}{\sqrt{9}}\text{ (by Rule 2)}\\=&\frac{2}{3}\end{aligned}

(f) \sqrt{\frac{50}{16}}

\begin{aligned}&\sqrt{\frac{50}{16}}\\=&\sqrt{\frac{25}{8}}\text{ (simplifying the fraction)}\\=&\frac{\sqrt{25}}{\sqrt{8}}\text{ (by Rule 2)}\\=&\frac{5}{\sqrt{8}}\\=&\frac{5}{\sqrt{4\times 2}}\\=&\frac{5}{\sqrt{4}\sqrt{2}}\text{ (by Rule 1)}\\=&\frac{5}{2\sqrt{2}}\end{aligned}

When a surd is multiplied by itself, we can used Rule 3 directly, in order to simplify.

Example 2: Simplify the following surds:

(a) \sqrt{5}\sqrt{5}

\begin{aligned}&\sqrt{5}\sqrt{5}\\=&5\text{ (by Rule 3)}\end{aligned}

(b) \sqrt{9}\sqrt{9}

\begin{aligned}&\sqrt{9}\sqrt{9}\\=&9\text{ (by Rule 3)}\end{aligned}

When we have a sum of terms involving surds, we collect like-terms in order to simplify. In real-life counting, if we have 4 apples plus 2 apples, this gives us 6 apples because we add  4 and 2. Similarly if we have 3 balls minus 1 ball, this gives us 2 balls because we deduct 1 from 2. Have a look at the following diagrams:

In algebra, this is represented as follows:

4a+2a=6a
3b-1b=2b

or

3b-b=2b

Example 3: Simplify the following expressions:

(a) 4\sqrt{3}+2\sqrt{3}

\begin{aligned}&4\sqrt{3}+2\sqrt{3}\\=&6\sqrt{3}\end{aligned}

(b) 3\sqrt{2}-\sqrt{2}

\begin{aligned}&3\sqrt{2}-\sqrt{2}\\=&3\sqrt{2}-1\sqrt{2}\\=&2\sqrt{2}\end{aligned}

(c) 2\sqrt{5}-7\sqrt{5}

\begin{aligned}&2\sqrt{5}-7\sqrt{5}\\=&-5\sqrt{5}\end{aligned}

(d) 3\sqrt{2}-\sqrt{8}

\begin{aligned}&3\sqrt{2}-\sqrt{8}\\=&3\sqrt{2}-\sqrt{4}\sqrt{2}\text{ (by Rule 1)}\\=&3\sqrt{2}-2\sqrt{2}\\=&\sqrt{2}\end{aligned}

(e) 5\sqrt{3}+\sqrt{7}+6\sqrt{3}-9\sqrt{7}

\begin{aligned}&5\sqrt{3}+\sqrt{7}+6\sqrt{3}-9\sqrt{7}\\=&5\sqrt{3}+6\sqrt{3}+\sqrt{7}-9\sqrt{7}\text{ (ordering terms)}\\=&11\sqrt{3}-8\sqrt{7}\end{aligned}

(f) 5\sqrt{2}+\sqrt{125}-2\sqrt{8}-2\sqrt{5}

\begin{aligned}&5\sqrt{2}+\sqrt{125}-2\sqrt{8}-2\sqrt{5}\\=&5\sqrt{2}-\sqrt{25}\sqrt{5}-2\sqrt{4}\sqrt{2}-2\sqrt{5}\text{ (by Rule 1)}\\=&5\sqrt{2}-5\sqrt{5}-8\sqrt{2}-2\sqrt{5}\\=&5\sqrt{2}-8\sqrt{2}-5\sqrt{5}-2\sqrt{5}\text{ (ordering terms)}\\=&-3\sqrt{2}-7\sqrt{5}\end{aligned}

Expressing surds as a single square root

This is the opposite of what we have done in simplifying surds. We are given a product of a whole number and a surd, and we want to express it as a single surd. We use the fact that a=\sqrt{a^2}

Example 4: Express the following as a single square root:

(a) 2\sqrt{5}

\begin{aligned}&2\sqrt{5}\\=&\sqrt{2^2}\sqrt{5}\\=&\sqrt{4}\sqrt{5}\\=&\sqrt{20}\text{ (by Rule 1)}\end{aligned}

(b) 3\sqrt{7}

\begin{aligned}&3\sqrt{7}\\=&\sqrt{3^2}\sqrt{7}\\=&\sqrt{9}\sqrt{7}\\=&\sqrt{63}\text{ (by Rule 1)}\end{aligned}

(c) 7\sqrt{3}

\begin{aligned}&7\sqrt{3}\\=&\sqrt{7^2}\sqrt{3}\\=&\sqrt{49}\sqrt{5}\\=&\sqrt{245}\text{ (by Rule 1)}\end{aligned}

(d) 5\sqrt{5}

\begin{aligned}&5\sqrt{5}\\=&\sqrt{5^2}\sqrt{5}\\=&\sqrt{25}\sqrt{5}\\=&\sqrt{125}\text{ (by Rule 1)}\end{aligned}

Expanding expressions involving Surds

In the case when we have an expression multiplied by a common factor, we multiply each term of the expression by the common factor.

Example 5: Expand the following:

(a) \sqrt{7}(2+\sqrt{5})

\begin{aligned}&\sqrt{7}(2+\sqrt{5})\\=&2\sqrt{7}+\sqrt{7}\sqrt{5}\end{aligned}

(b) \sqrt{7}(2\sqrt{3}-2\sqrt{7})

\begin{aligned}&\sqrt{7}(2\sqrt{3}-2\sqrt{7})\\=&2\sqrt{7}\sqrt{3}-2\sqrt{7}\sqrt{7}\\=&2\sqrt{7}\sqrt{3}-2(7)\text{ (by Rule 3)}\\=&2\sqrt{7}\sqrt{3}-14\end{aligned}

In the case when we have two expressions multiplied by each other, we multiply each term of the first expression with each term of the second expression. For example, if we are given:

(\sqrt{3}-\sqrt{2})(\sqrt{3}-\sqrt{2})

We must perform the following 4 multiplications, which will give us 4 terms.

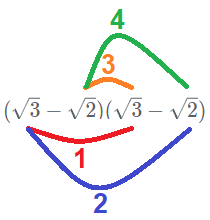
Hence,

\begin{aligned}&(\sqrt{3}-\sqrt{2})(\sqrt{3}-\sqrt{2})\\=&\sqrt{3}\sqrt{3}-\sqrt{3}\sqrt{2}-\sqrt{2}\sqrt{3}+\sqrt{2}\sqrt{2}\text{ (performing the 4 multiplications)}\\=&\sqrt{3}\sqrt{3}-\sqrt{2}\sqrt{3}-\sqrt{2}\sqrt{3}+\sqrt{2}\sqrt{2}\text{ (switching the factors in the 3rd term)}\\=&\sqrt{3}\sqrt{3}-2\sqrt{2}\sqrt{3}+\sqrt{2}\sqrt{2}\text{ (collecting like-terms)}\\=&3-2\sqrt{2}\sqrt{3}+2\text{ (by Rule 3)}\\=&5-2\sqrt{2}\sqrt{3}\end{aligned}

Example 6: Expand the following:

(a) (4-\sqrt{7})(5+2\sqrt{7})

\begin{aligned}&(4-\sqrt{7})(5+2\sqrt{7})\\=&20+8\sqrt{7}-5\sqrt{7}-2\sqrt{7}\sqrt{7}\\=&20+3\sqrt{7}-2\sqrt{7}\sqrt{7}\text{ (collecting like-terms)}\\=&20+3\sqrt{7}-14\text{ (by Rule 3)}\\=&6+3\sqrt{7}\end{aligned}

(a) (2\sqrt{5}+6\sqrt{3})(\sqrt{5}-\sqrt{3})

\begin{aligned}&(2\sqrt{5}+6\sqrt{3})(\sqrt{5}-\sqrt{3})\\=&2\sqrt{5}\sqrt{5}-2\sqrt{5}\sqrt{3}+6\sqrt{3}\sqrt{5}-6\sqrt{3}\sqrt{3}\\=&2\sqrt{5}\sqrt{5}-2\sqrt{3}\sqrt{5}+6\sqrt{3}\sqrt{5}-6\sqrt{3}\sqrt{3}\text{ (switching the factors of the second term)}\\=&2\sqrt{5}\sqrt{5}+4\sqrt{3}\sqrt{5}-6\sqrt{3}\sqrt{3}\text{ (collecting like-terms)}\\=&10+4\sqrt{3}\sqrt{5}-18\text{ (by Rule 3)}\\=&-8+4\sqrt{3}\sqrt{5}\end{aligned}

(c) (2-\sqrt{5})(2+\sqrt{5})

\begin{aligned}&(2-\sqrt{5})(2+\sqrt{5})\\=&4+2\sqrt{5}-2\sqrt{5}-\sqrt{5}\sqrt{5}\\=&4-\sqrt{5}\sqrt{5}\sqrt{7}\text{ (collecting like-terms)}\\=&4-5\text{ (by Rule 3)}\\=&-1\end{aligned}

(d) (\sqrt{a}+\sqrt{b})(\sqrt{a}-\sqrt{b})

\begin{aligned}&(\sqrt{a}+\sqrt{b})(\sqrt{a}-\sqrt{b})\\=&\sqrt{a}\sqrt{a}-\sqrt{a}\sqrt{b}+\sqrt{b}\sqrt{a}-\sqrt{b}\sqrt{b}\\=&\sqrt{a}\sqrt{a}-\sqrt{a}\sqrt{b}+\sqrt{a}\sqrt{b}-\sqrt{b}\sqrt{b}\text{ (switching the factors of the third term)}\\=&\sqrt{a}\sqrt{a}-\sqrt{b}\sqrt{b}\text{ (collecting like-terms)}\\=&a-b\text{ (by Rule 3)}\end{aligned}

Note that in Examples 6 (c) and (d), there are no surds in the answer. This results from the fact that the two expressions in the brackets are identical except for the fact that their second term has an opposite sign. We will use this fact in the next section on rationalising the denominator.

Rationalising the Denominator

Here we are given a fraction in which there are surds in the denominator. We use algebra in order to express the fraction in a way that does not contain surds in the denominator. We are making the denominator a rational number, hence the title: “rationalise” the denominator. We are going to consider 3 cases. When the denominator has the form:

Case 1: \sqrt{a}: then we multiply both the numerator and denominator by \sqrt{a}

Case 2: a\sqrt{b}+c\sqrt{d}: then we multiply both the numerator and denominator by a\sqrt{b}-c\sqrt{d}

Case 3: a\sqrt{b}-c\sqrt{d}: then we multiply both the numerator and denominator by a\sqrt{b}+c\sqrt{d}

Note that Case 2 and Case 3, are similar, just remember to multiply by the same expression after switching the sign of the second term.

Example 7: Rationalise the denominator (Case 1):

(a) \frac{1}{\sqrt{2}}

\begin{aligned}&\frac{1}{\sqrt{2}}\\=&\frac{1\sqrt{2}}{\sqrt{2}\sqrt{2}}\\=&\frac{1\sqrt{2}}{2}\text{ (by Rule 3)}\\=&\frac{\sqrt{2}}{2}\end{aligned}

(b) -\frac{3}{\sqrt{3}}

\begin{aligned}&-\frac{3}{\sqrt{3}}\\=&-\frac{3\sqrt{3}}{\sqrt{3}\sqrt{3}}\\=&-\frac{3\sqrt{3}}{3}\text{ (by Rule 3)}\\=&-\frac{\sqrt{3}}{1}\text{ (simplifying fraction)}\\=&-\sqrt{3}\end{aligned}

(c) \sqrt{\frac{3}{2}}

\begin{aligned}&\sqrt{\frac{3}{2}}\\=&\frac{\sqrt{3}}{\sqrt{2}}\text{ (by Rule 2)}\\ =&\frac{\sqrt{3}\sqrt{2}}{\sqrt{2}\sqrt{2}}\\=&\frac{\sqrt{3}\sqrt{2}}{2}\text{ (by Rule 3)}\end{aligned}

Example 8: Rationalise the denominator (Cases 2 & 3):

(a) \frac{2}{1+\sqrt{2}}

\begin{aligned}&\frac{2}{1+\sqrt{2}}\\=&\frac{2(1-\sqrt{2})}{(1+\sqrt{2})(1-\sqrt{2})}\\=&\frac{2(1-\sqrt{2})}{1+\sqrt{2}-\sqrt{2}-\sqrt{2}\sqrt{2}}\text{ (expanding the denominator)}\\=&\frac{2(1-\sqrt{2})}{1-2}\text{ (simplifying the denominator)}\\=&\frac{2(1-\sqrt{2})}{-1}\\=&-2(1-\sqrt{2})\\=&-2+2\sqrt{2}\end{aligned}

(b) \frac{\sqrt{5}}{1-\sqrt{3}}

\begin{aligned}&\frac{\sqrt{5}}{1-\sqrt{3}}\\=&\frac{\sqrt{5}(1+\sqrt{3})}{(1-\sqrt{3})(1+\sqrt{3})}\\=&\frac{\sqrt{5}(1+\sqrt{3})}{1-\sqrt{3}+\sqrt{3}-\sqrt{3}\sqrt{3}}\text{ (expanding the denominator)}\\=&\frac{\sqrt{5}(1+\sqrt{3})}{1-3}\text{ (simplifying the denominator)}\\=&\frac{\sqrt{5}(1+\sqrt{3})}{-2}\\=&-\frac{\sqrt{5}(1+\sqrt{3})}{2}\end{aligned}

(c) \frac{\sqrt{5}}{\sqrt{3}+\sqrt{2}}

\begin{aligned}&\frac{\sqrt{5}}{\sqrt{3}+\sqrt{2}}\\=&\frac{\sqrt{5}(\sqrt{3}-\sqrt{2})}{(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})}\\=&\frac{\sqrt{5}(\sqrt{3}-\sqrt{2})}{\sqrt{3}\sqrt{3}-\sqrt{3}\sqrt{2}+\sqrt{2}\sqrt{3}-\sqrt{2}\sqrt{2}}\text{ (expanding the denominator)}\\=&\frac{\sqrt{5}(\sqrt{3}-\sqrt{2})}{3-2}\text{ (simplifying the denominator)}\\=&\frac{\sqrt{5}(\sqrt{3}-\sqrt{2})}{1}\\=&\sqrt{5}(\sqrt{3}-\sqrt{2})\end{aligned}

(d) \frac{\sqrt{5}}{\sqrt{5}-3\sqrt{2}}

\begin{aligned}&\frac{\sqrt{5}}{\sqrt{5}-3\sqrt{2}}\\=&\frac{\sqrt{5}(\sqrt{5}+3\sqrt{2})}{(\sqrt{5}-3\sqrt{2})(\sqrt{5}+3\sqrt{2})}\\=&\frac{\sqrt{5}(\sqrt{5}+3\sqrt{2})}{\sqrt{5}\sqrt{5}+3\sqrt{5}\sqrt{2}-3\sqrt{2}\sqrt{5}-9\sqrt{2}\sqrt{2}}\text{ (expanding the denominator)}\\=&\frac{\sqrt{5}(\sqrt{5}+3\sqrt{2})}{5-9(2)}\text{ (simplifying the denominator)}\\=&\frac{\sqrt{5}\sqrt{5}+3\sqrt{5}\sqrt{2}}{-13}\\=&-\frac{5+3\sqrt{5}\sqrt{2}}{13}\end{aligned}