Types of Numbers
Matsec Syllabus: Pure Mathematics Paper 1 Topic 1: Classification of Numbers: \mathbb{R}, \mathbb{C}, \mathbb{N}, \mathbb{Q}, \mathbb{Z}.
The most common types of numbers are the followings:
- Real Numbers (\mathbb{R})
- Rational Numbers (\mathbb{Q})
- Irrational Numbers (\mathbb{I})
- Natural Numbers (\mathbb{N})
- Whole Numbers (also known as Integers) (\mathbb{Z})
- Complex Numbers (\mathbb{C})
In the list above, the letter symbol in brackets is used to refer to the particular type of number. We are going to learn the difference between these types of numbers and be able to decide whether or not a given number follows a particular type/class of numbers.
Real Numbers (\mathbb{R})
Real numbers are sometimes called “measurement” numbers. These are numbers obtained from measuring something. Think about measuring height (altitude), temperature, time etc.., what numbers can you possibly get?
These are numbers which can be written as decimal, i.e. with a list of digits after the decimal point.
Examples:
(1) 0.5
(2) 1.35
(3) 30.24342
(4) -44.5
(5) 4
(6) \frac{24}{35}
(7) \pi
Notes:
- A real number can be negative (as in Example (4)).
- A fraction is always real number because it can be written in decimal form. In Example (6), \frac{24}{35} can be written as 0.685714285714286. It is a real number.
- Even though a number has no decimals after the point (i.e. it is a whole number), it is still a real number. In Example (5), 4 can be written as 4.000, and is therefore a real number.
- In Example (7), the number \pi is a real number because it can be written in decimal form as 3.141592653589793… even though the digits after the decimal point never end!
- Basically all the numbers that you met so far are real numbers! Numbers that are not real numbers are called Complex Numbers, which are briefly introduced below and will be analysed later on, in the A level Topic on Complex Numbers.
Real numbers are divided into two types: Rational numbers & Irrational number. A real number can be either Rational or Irrational but not both!
Rational Numbers (\mathbb{Q})
Rational number are real numbers that can be expressed as a fraction of two integers.
Examples:
(1) 0.5
(2) 30.24342
(3) -44.5
(4) 7
(5) 3.\dot{3}
(6) 3.\dot{3}7\dot{5}
Notes:
- Any number with a finite (limited) number of digits after the decimal point can be written as a fraction of two integers, and is thus a rational number. In Example (1), 0.5 can be written as \frac{1}{2} and thus it is a rational number. In Example (2), 30.24342 can be written as \frac{3024342}{100000} and thus it is a rational number. (Note the number of zeros in the denominator is the same as the number of decimal places).
- A rational number can be negative, like the one given in Example (3). The number -44.5 can be expressed as a fraction \frac{-445}{10}.
- A whole number (integer) is always a rational number. In Example (4), the number 7 can be expressed as \frac{7}{1} and is therefore a rational number.
- Any number that has an infinite (unlimited) number of decimal places, but has a repeating pattern is a rational numbers. In Example (5), 3.\dot{3} can be expressed as \frac{10}{3}. Similarly, in Example (6), 3.\dot{3}7\dot{5} can be expressed as \frac{3372}{999}. The interested reader can check the article on converting any recurring decimal into a fraction!
Irrational Numbers (\mathbb{I})
Rational number are real numbers that CANNOT be expressed as a fraction of two integers. The rational numbers defined above seem to cover lots of possible cases of how a number could be expressed. So which are irrational numbers?
Irrational numbers are numbers that have an infinite number of decimal places without a repeating pattern! Otherwise a number would always be rational.
The following are typical numbers that you could always refer to as examples of irrational numbers.
Examples:
(1) \pi
(2) e
(3) \ln(2)
(4) \sqrt{2},\sqrt{3},\sqrt{5},\sqrt{6},etc…
Notes:
- In order to get an idea of the numeric values: \pi=3.1415926535897932… and e (known as Euler’s number) is equal to 2.7182818…
- The function \ln is known as the natural logarithm. Logarithms are analysed in further detail later on.
- The numbers listed as Example (4) are known as surds. For manipulation and simplification of surds, check the A level topic on Surds.
Natural Numbers (\mathbb{N})
Natural numbers arise from counting. Imagine you are counting cars, trees, people, apples, or any physical object. When you spot the first item, you say “One!”, when you spot the second item you say “Two!” and so on. Therefore the natural numbers are:
Notes:
- The natural numbers do not have any decimal places, i.e. they are “whole”.
- The number 0 is NOT natural number (because you cannot count something that cannot exist!).
- Natural numbers cannot be negative.
Whole Numbers (Integers) (\mathbb{Z})
Whole numbers are numbers without a fractional part. They have no decimal places. Whole numbers are made of the natural numbers, their negatives and the number 0. Thus the whole numbers are:
Notes:
- \mathbb{Z}^+ is used to denote the positive whole numbers, namely: 1,2,3,4,5,…
- \mathbb{Z}^- is used to denote the negative whole numbers, namely: -1,-2,-3,-4,-5,…
Complex Numbers (\mathbb{C})
Complex Numbers are numbers that are NOT real numbers. These arise from the expression \sqrt{-1}. Complex numbers are studied thoroughly in A level with a whole chapter dedicated just to this type kind of numbers.
Summary Chart of Numbers
The following chart gives an overview of the types of numbers and describes the relationships between them.
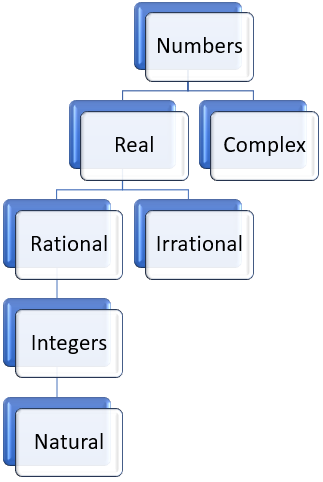
- Numbers are split into two categories: Real and Complex
- Real Numbers are split into two categories: Rational and Irrational
- A category that is linked to a category above shows that it is a subset of the category above it. For example:
- A rational number is also a real number
- An integer is also a rational number
- An integer is also a real number
- A natural number is also an integer